Mot de passe oublié ?

Jeux Exercices Cours Quiz À imprimer Tables Activités Enigmes
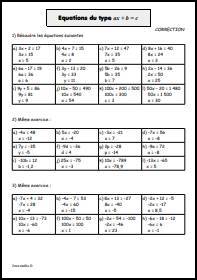
Résoudre une équation produit nul

Calculer l'image ou l'antécédent d'un nombre par une fonction affine
Problèmes conduisant à la résolution d'une équation du type ax+b=cx+d
Théorème de Thalès
Puissances de 10 et préfixes
Signe d'une fonction affine
Lire les coordonnées des sommets d'un pavé droit

Précedent :
Utilisation de la racine carrée d'un produit
L'objectif de cet exercice est la résolution d'équations du type (ax + b)(cx + d)=0 appelées équations produit nul.
Rappelons la propriété suivante : un produit de facteurs est nul si et seulement si au moins un des facteurs est nul. Résoudre une équation de ce type revient donc à résoudre autant d'équations que de facteurs.
Exemple : Résoudre (2x - 6)(x + 5)=0 revient à résoudre chacune des équations 2x - 6 = 0 et x + 5 = 0. L'équation admet donc 2 solutions : 3 et -5.
Cours et autres exemples : Equations produit nul
Suivant :
Résoudre une équation se ramenant à une équation produit nul

Fiches d'exercices PDF à imprimer :
Equations - le pingouin
Equations - le pingouin
Equations - le pingouin - Correction
Equations - le pingouin - Correction
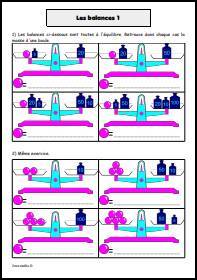
Equations - les balances 1
Equations - les balances 1
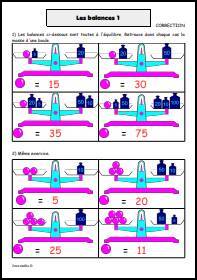
Equations - les balances 1 - Correction
Equations - les balances 1 - Correction
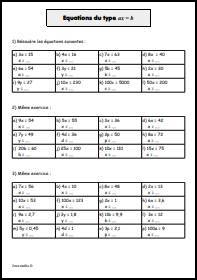
Equations du type a+x=b
Equations du type a+x=b
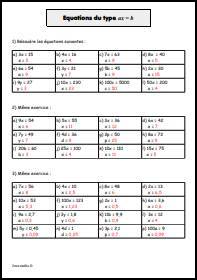
Equations du type a+x=b Correction
Equations du type a+x=b Correction
Equations du type ax=b
Equations du type ax=b
Equations du type ax=b - Correction
Equations du type ax=b - Correction
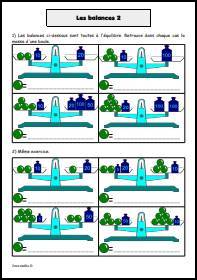
Equations - les balances 2
Equations - les balances 2
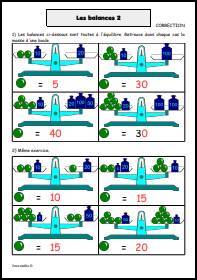
Equations - les balances 2 - Correction
Equations - les balances 2 - Correction
Equations du type ax+b=c
Equations du type ax+b=c
Equations du type ax+b=c - Correction
Equations du type ax+b=c - Correction
Equations du type ax+b=cx+d
Equations du type ax+b=cx+d
Equations du type ax+b=cx+d - Correction
Equations du type ax+b=cx+d - Correction
Equations se ramenant à une équation du type ax+b=cx+d
Equations se ramenant à une équation du type ax+b=cx+d
Equations se ramenant à une équation du type ax+b=cx+d - Cor
Equations se ramenant à une équation du type ax+b=cx+d - Cor
Problèmes
Problèmes
Problèmes - Correction
Problèmes - Correction
Equations produit nul
Equations produit nul
Equations produit nul - Correction
Equations produit nul - Correction



Factoriser avec les identités remarquables
Lire l'abscisse d'un point sur une droite graduée
Résoudre un problème mettant en jeu la divisibilité
Calculer la somme de deux nombres relatifs
Utiliser la somme des angles dans un triangle particulier
Expression analytique du produit scalaire