Cours : Variations de fonctions

Définitions :
Soit f une fonction définie sur un intervalle I de ℝ.
Soit C sa courbe représentative.

Fonction croissante :
f est une fonction croissante sur I si pour tous nombres réels a et b de I, on a :

Si a ≤ b, alors f(a) ≤ f(b)

Exemple :

La courbe représentative d'une fonction croissante «monte de gauche à droite».

Une fonction croissante conserve l'ordre.

Fonction décroissante :
f est une fonction décroissante sur I si pour tous nombres réels a et b de I, on a :

Si a ≤ b, alors f(a) ≥ f(b)

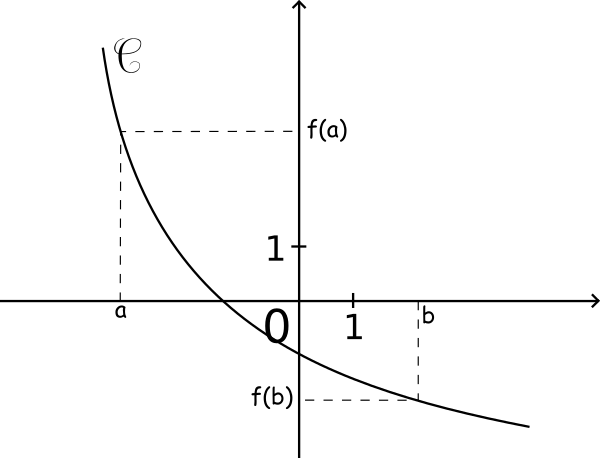
Exemple :

La courbe représentative d'une fonction décroissante «descend de gauche à droite».

Une fonction décroissante change l'ordre.

Extremum d'une fonction :
Soit f une fonction définie sur un intervalle I de ℝ et a un nombre réel de I.

Définitions :
• f(a) est le maximum de f sur I si f(x) ≤ f(a) pour tout x de I.
• f(a) est le minimum de f sur I si f(x) ≥ f(a) pour tout x de I.
• f(a) est un extremum de f sur I si f(a) est un maximum ou un minimum.

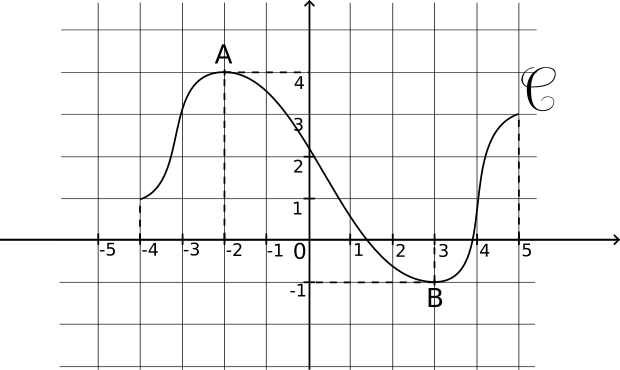
Exemple : La courbe C ci-dessous représente une fonction f définie sur [-4;5].

Le point A(-2;4) est le plus «haut» de la courbe sur [-4;5]. Le maximum de f sur [-4;5] est 4 atteint en -2.

Le point B(3;-1) est le plus «bas» de la courbe sur [-4;5]. Le minimum de f sur [-4;5] est -1 atteint en 3.

Tableau de variations :
Soit f une fonction définie sur un intervalle I de ℝ.
On peut résumer les variations de f dans un tableau de variations.

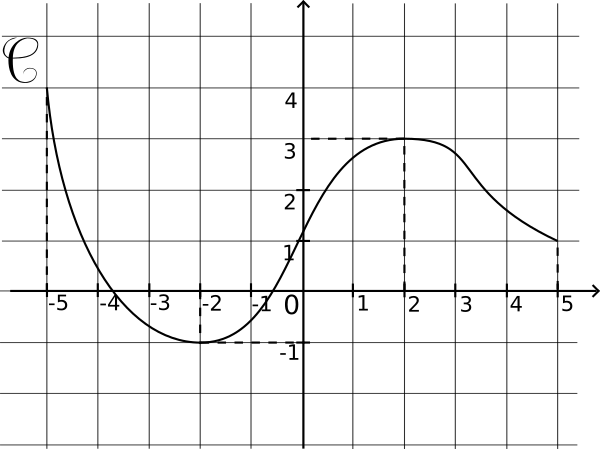
Exemple : La courbe C ci-dessous représente une fonction f définie sur [-5;5].

Tableau de variations de f

Résolution graphique d'inéquations :
Soient f et g deux fonctions définies sur un intervalle I de ℝ. On note C_f et C_g leur courbe représentative dans un repère du plan.

1) Inéquations du type f(x)>k (avec k réel).
Soit k ∈ ℝ. Les solutions de l'inéquation f(x) > k (respectivement f(x) < k )sont les abscisses des points de la courbe C_f situés au-dessus (respectivement en dessous) de la droite d'équation y=k.
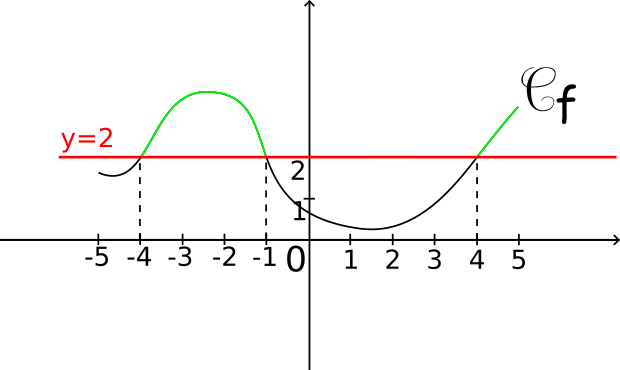
Exemple : Résoudre graphiquement l'inéquation f(x)>2

Les solutions de l'inéquation f(x)>2 sont les abscisses des points de la courbe C_f situés au-dessus la droite d'équation y=2. L'ensemble solution S₁ de cette inéquation est donc S₁=]-4;-1[∪]4;5].

Remarque : les nombres -4; -1 et 4 sont exclus de l'ensemble solution car f(x) doit être strictement supérieur à 2 et f(-4)=f(-1)=f(4)=2.

2) Inéquations du type f(x)>g(x).
Les solutions de l'inéquation f(x) > g(x) sont les abscisses des points de la courbe C_f situés au dessus de C_g.
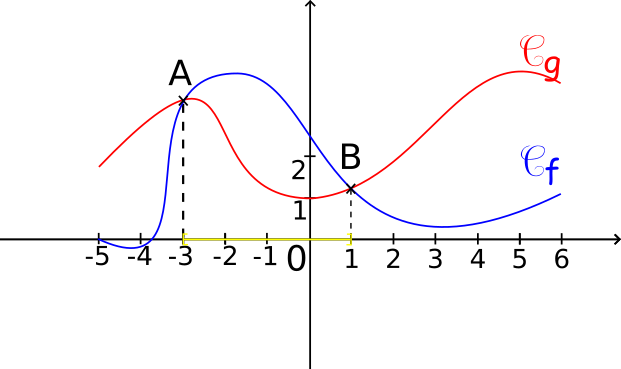
Exemple : Résoudre graphiquement l'inéquation f(x) ≥ g(x)

La courbe C_f est au-dessus de la courbe C_g sur l'intervalle [-3;1]. L'ensemble solution S₂ de cette inéquation est donc S₂=[-3;1].

Tableau de signes :
Soit f une fonction définie sur un intervalle I de ℝ et C_f sa courbe représentative dans un repère du plan.

• f(x)>0 si et seulement si le point M(x;f(x)) est au-dessus de l'axe des abscisses.
• f(x)<0 si et seulement si le point M(x;f(x)) est en dessous de l'axe des abscisses.
On résume le signe d'une fonction dans un tableau de signes.

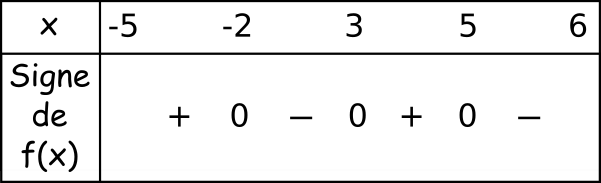
Exemple : Donner le tableau de signes de la fonction f représentée ci-dessous.