On considère la série statistique définie par le tableau suivant :
| Valeur |
x1 |
x2 |
... |
xp |
| Effectif |
n1 |
n2 |
... |
np |
L'effectif total de cette série est N = n
1 + n
2 + ... + n
p
Rappel :
La
moyenne de cette série statistique est le nombre réel
‾x tel que :
‾x=n1x1+n2x2+...+npxpN
Définitions :
•
La
variance d'une série statistique est le nombre réel, noté V, défini par :
V=n1(x1-‾x)2+n2(x2-‾x)2+...+np(xp-‾x)2N
• L'
écart-type d'une série statistique est le nombre réel, noté σ, défini par σ =
√V.
La variance et l'écart-type sont des
paramètres de dispersion d'une série statistique.
L'avantage de l'écart-type est de s'exprimer dans la même unité que les
xi
Exemple :
Les notes obtenues par les élèves d'une classe de première ES au dernier devoir de mathématiques ont été récapitulées dans le tableau ci-dessous:
| Note |
5 |
7 |
9 |
10 |
11 |
12 |
13 |
15 |
17 |
| Effectif |
2 |
3 |
1 |
5 |
7 |
7 |
4 |
1 |
2 |
‾x=2×5+3×7+1×9+5×10+7×11+7×12+4×13+1×15+2×172+3+1+5+7+7+4+1+2=35232=11
La moyenne du devoir est de 11
V=2×(5-11)2+3×(7-11)2+1×(9-11)2+5×(10-11)2+7×(11-11)2+7×(12-11)2+4×(13-11)2+1×(15-11)2+2×(17-11)232
V=2×36+3×16+1×4+5×1+7×0+7×1+4×4+1×16+2×3632
V=72+48+4+5+0+7+16+16+7232=24032=7,5
La variance de cette série est égale à 7,5 et l'écart-type σ =
√7,5 ≈ 2,74
Utilisation de la calculatrice :
-> Avec le mode stat des modèles Casio :
1) Choisir le menu stat et compléter les deux premières colonnes list1 et list2 par les valeurs de la série
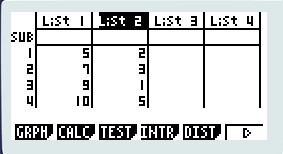
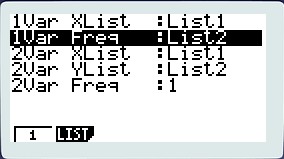
2) Choisir calc (f2) puis Set (f6) puis choisir List1 pour la ligne 1Var Xlist et List2 pour la ligne 1Var Freq
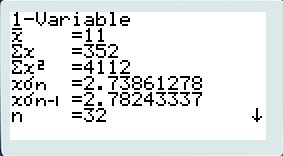
3) Taper exit puis 1var (f1), lire les valeurs de la moyenne et de l'écart-type (xσn) ici : 2.73861278
-> Avec la touche Stat des modèles TI :
1) Taper la touche Stat puis edit (1)
2) Compléter les deux premières colonnes (L1 et L2)
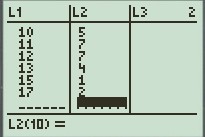
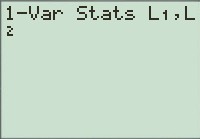
3) Taper Stat puis choisir calc puis 1-Var stats L1,L2
4) Il suffit alors lire les valeurs de la moyenne et de l'ecart-type (noté σx) ici : 2.738612788
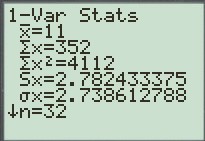
Remarque : La calculatrice ne fournit pas la valeur de la variance, pour la retrouver, il suffit d'élever la valeur de l'écart-type au carré.












