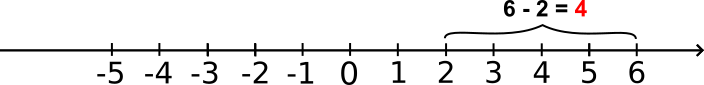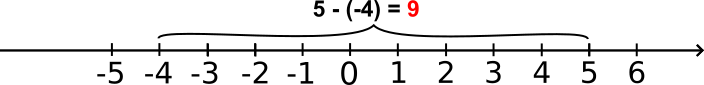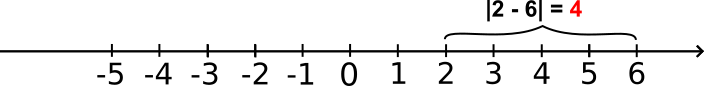Distance entre deux nombres

Définition : Soient a et b, deux nombres réels.
• Si a ≤ b, la distance entre a et b est égale à b - a
• Si b ≤ a, la distance entre a et b est égale à a - b

Exemples :
1) La distance entre 2 et 6 est égale à 4.

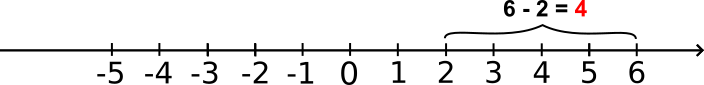
2) La distance entre 5 et -4 est égale à 9.

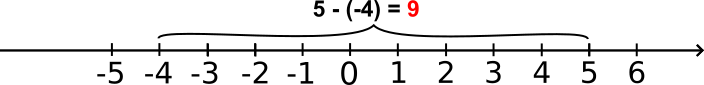
Valeur absolue d'un nombre réel

Définition : Soit a un nombre réel, on appelle valeur absolue de a la distance à 0 de a. La valeur absolue de a est notée |a|.

Exemples :
|7| = 7 ; |-2,5| = 2,5 ; |13| = 13 ; |-5,4| = 5,4

Propriétés :
Soit a un nombre réel :
• |a| = 0 équivaut à a = 0;
• si a ≥ 0, |a| = a;
• si a ≤ 0, |a| = -a;

Valeur absolue et distance

Propriété : Quels que soient les réels a et b, la valeur absolue de a - b est égale à la distance de a à b.

Exemples :
1) |2 - 6| = 4.


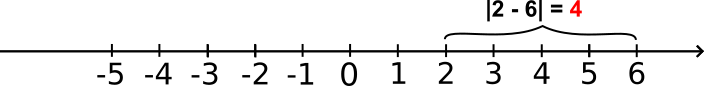
2) |-4 - 5| = 9.

Equations comportant des valeurs absolues

Soient a et x des nombres réels.

1) Equations du type |x| = a
• Si a < 0 , pas de solution
• Si a = 0 , x = 0
• Si a > 0 , x = a ou x = -a

Exemples :
a) |x| = -4 => pas de solution.
b) |x + 3| = 5 => x + 3 = 5 ou x + 3 = -5 donc x = 2 ou x = -8.

2) Equations du type |x| = |a|
• x = a ou x = -a

Exemple :
|2x + 2| = |x - 4| => 2x + 2 = x - 4 ou 2x + 2 = -(x - 4) donc x = -6 ou x = 2/3

Inéquations comportant des valeurs absolues

Soient a, b et x des nombres réels.

1) Inéquations du type |x| ≤ a
• Si a < 0 , pas de solution
• Si a = 0 , x = 0
• Si a > 0 , -a ≤ x ≤ a ( c'est à dire x ∈ [-a;a] )

Exemples :
a) |x| < -1 => pas de solution.
b) |x| ≤ 2 => -2 ≤ x ≤ 2 (c'est à dire x ∈ [-2;2]).

2) Inéquations du type |x - b| ≤ a
• Si a < 0 , pas de solution
• Si a = 0 , x = b
• Si a > 0, b - a ≤ x ≤ b + a ( c'est à dire x ∈ [b-a;b+a] )

Exemples :
a) |x + 1| < -7 => pas de solution.
b) |x - 1| ≤ 2 => -2 ≤ x - 1 ≤ 2 donc -1 ≤ x ≤ 3 (c'est à dire x ∈ [-1;3]).