Cours : Triangles semblables

Définition : Deux triangles sont dits semblables ou de même forme, s'ils ont les angles deux à deux de même mesure.
Exemple :

\hat{ABC} = \hat{DEF}

\hat{BAC} = \hat{EDF}

\hat{BCA} = \hat{EFD}

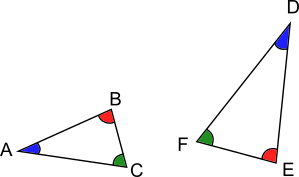
ABC et DEF sont deux triangles semblables.

Vocabulaire : Lorsque deux triangles sont semblables :
• Les angles égaux sont dits homologues
• Les côtés opposés à des angles égaux sont dits homologues
• Les sommets des angles égaux sont dits homologues

Angles homologues	Sommets homologues	Côtés homologues
$\hat{ABC}$ et $\hat{DEF}$	B et E	[AC] et [DF]
$\hat{BAC}$ et $\hat{EDF}$	A et D	[BC] et [EF]
$\hat{BCA}$ et $\hat{EFD}$	C et F	[AB] et [DE]

Remarque : Pour montrer que deux triangles sont semblables il suffit de montrer que deux angles d'un triangle soient égaux à deux angles d'un autre triangle. En effet, puisque la somme des angles d'un triangle est égale à 180°, si deux angles sont deux à deux de même mesure, il en est de même pour le troisième angle de chaque triangle.

Exemple :

\hat{BAC} = \hat{EDF} = 22°

\hat{DEF} = \hat{ABC} = 114°

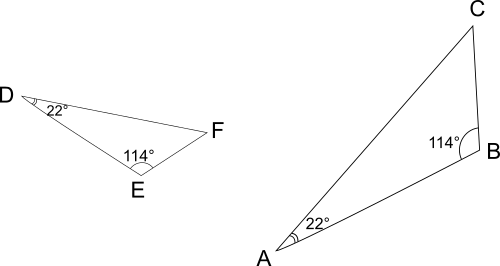
ABC et DEF ont deux angles égaux deux à deux donc ils sont semblables.

Remarque : on verifie facilement par le calcul que les deux derniers angles ont bien la même mesure :

\hat{ACB} = 180 - 114 - 22 = 44° et

\hat{DFE} = 180 - 114 -22 = 44°

Propriété des longueurs :
Si les longueurs des côtés d'un triangle sont proportionnelles aux longueurs d'un autre triangle, alors ces deux triangles sont semblables.

Exemple :

\frac{RS}{KM} = \frac{6}{4} = 1,5

\frac{RT}{LM} = \frac{7,5}{5} = 1,5

\frac{ST}{KL} = \frac{3}{2} = 1,5

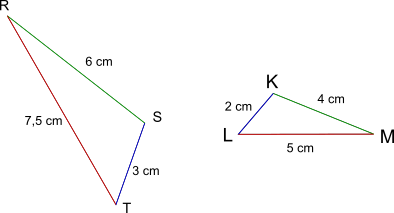
En divisant la longueur de chaque côté du triangle RST par la longueur de son côté homologue dans le triangle KLM, on obtient toujours le même résultat : 1,5. Les longueurs des côtés des deux triangles sont donc proportionnelles et les triangles RST et KLM sont semblables. Le triangle RST est un agrandissement du triangle KLM.

Propriété réciproque :
Si deux triangles sont semblables, alors les longueurs des côtés d'un des triangles sont proportionnelles aux longueurs des côtés de l'autre triangle.

Exemple :
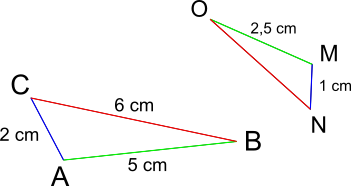
ABC et OMN sont deux triangles semblables. Calculer la longueur du côté [ON].

\frac{CA}{MN} = \frac{2}{1} = 2

donc ON = 6 ÷ 2 = 3.
donc ON = 3 cm.

Propriété :
Si deux triangles ont un angle de même mesure compris entre deux côtés dont les longueurs sont proportionnelles, alors ces triangles sont semblables.

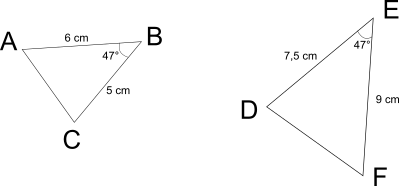
Exemple :

\frac{DE}{BC} = \frac{7,5}{5} = 1,5

\frac{EF}{AB} = \frac{9}{6} = 1,5

Les longueurs AB et BC sont proportionnelles aux longueurs DE et EF, de plus

\hat{ABC}

\hat{DEF}

, donc les triangles ABC et DEF sont semblables.