Cours : Statistiques

Effectifs :
Définition : Dans une série de données, l'effectif d'une donnée est le nombre de fois où elle apparaît. L'effectif total est le nombre total de valeurs de la série.
Exemple :
Une enquête réalisée sur les activités sportives préférées des élèves d'un collège a donné les résultats suivants :

Activité préférée	Football	Tennis	Basketball	Handball	Rugby	Total
Effectif	103	40	54	22	81	300

L'effectif des élèves préférant le tennis est 40, ce qui signifie que 40 élèves préfèrent le tennis.
L'effectif total est 300, il s'agit du nombre d'élèves du collège.

Fréquences :
Définition : La fréquence d'une donnée est le quotient de son effectif par l'effectif total.
Exemple :
Reprenons le tableau précédent en ajoutant des lignes pour les fréquences:

Activité préférée	Football	Tennis	Basketball	Handball	Rugby	Total
Effectif	103	40	54	22	81	300
Fréquence	$\frac{103}{300}$	$\frac{40}{300}$	$\frac{54}{300}$	$\frac{22}{300}$	$\frac{81}{300}$	$\frac{300}{300} = 1$
Fréquence en % (arrondi à 0,1% près)	34,3	13,3	18	7,3	27	100

La fréquence des élèves préférant le rugby est égale à 0,27. Pour exprimer cette fréquence en pourcentage, il suffit de multiplier ce résultat par 100, on obtient donc 27%.
La fréquence de l'effectif total doit être égale à 1. Dans notre exemple, si on ajoute les pourcentages de chaque donnée, on obtient 99,9% à cause des arrondis.

Représentation de données :

1) Diagramme en barres :

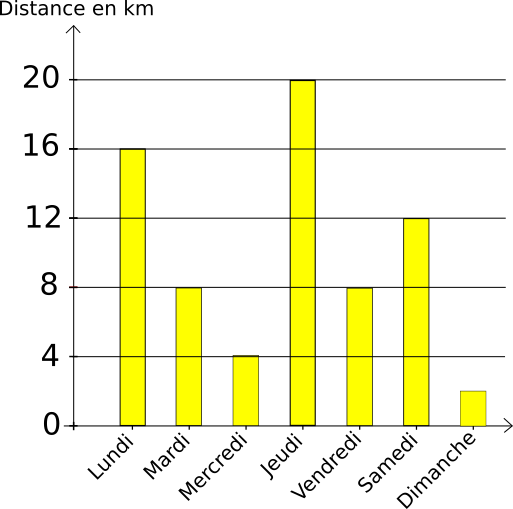
Le diagramme en barres permet de voir rapidement la valeur qui a le plus grand effectif. L'exemple ci-contre représente la distance en km parcourue par un cycliste selon le jour de la semaine. On remarque que c'est le jeudi qu'il a parcouru la plus grande distance : 20km.

2) Diagramme circulaire :

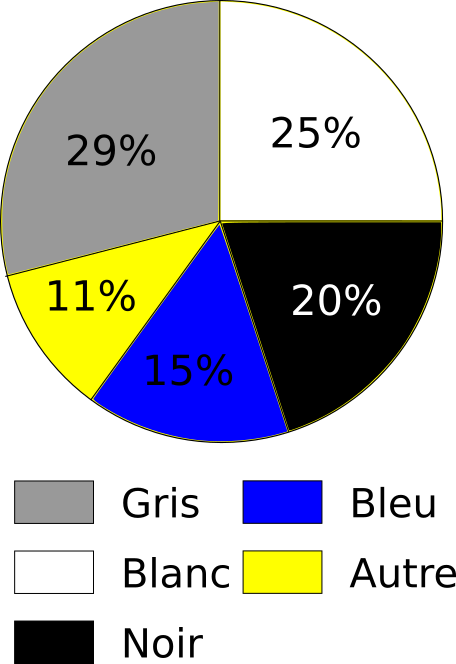
Le diagramme circulaire donne une vision globale de la répartition des données d'une série statistique. Il est particulièrement adapté pour une série de données à caractère qualitatif. L'exemple ci-contre donne la répartition des voitures selon leurs couleurs dans une certaine ville. On constate par exemple que 25% des voitures de cette ville sont blanches.
Pour déterminer la mesure de l'angle de chaque secteur angulaires, on utilise un tableau de proportionnalité :

Couleur	Gris	Blanc	Noir	Bleu	Autre	Total
Fréquence (en %)	29	25	20	15	11	100
Angle (en °)	104,4	90	72	54	39.6	360

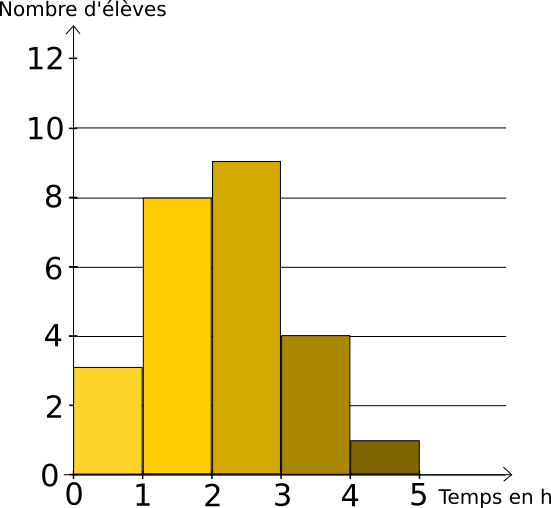
3) Histogramme :

L'histogramme permet de rendre les données plus lisibles en effectuant un regroupement de données par classes. Ce type de représentation est adaptée lorsque les données sont très variées.
L'exemple ci-contre donne le temps passé par jour sur internet par les élèves d'une classe de quatrième. On constate par exemple que 8 élèves de cette classe passent entre 1h et 2h sur internet par jour. Pour trouver le nombre d'élèves de la classe, c'est à dire, l'effectif total, il faut additionner les effectifs de chaque tranche horaire : 3 + 8 + 9 + 4 + 1 = 25. Il y a donc 25 élèves dans la classe.