Définition :
Dans un
parallélépipède rectangle, un
repère est formé par un sommet (appelé origine du repère) et trois droites (appelées axes du repère) portées par les arêtes issues de l’origine.
Exemple :
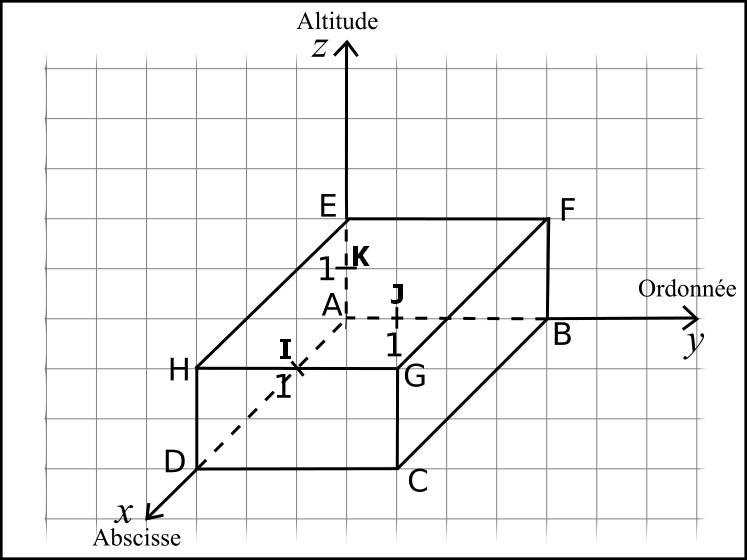
Dans l'exemple ci-dessous, on considère le repère (A , (AI) , (AJ) , (AK) ).
L’origine du repère est le sommet A
L’axe des abscisses est porté par la droite (AI)
L’axe des ordonnées est porté par la droite (AJ)
L’axe des altitudes est porté par la droite (AK)
Le point A a pour coordonnées (0 ; 0 ; 0)
Le point B a pour coordonnées (0 ; 4 ; 0)
Le point C a pour coordonnées (3 ; 4 ; 0)
Le point D a pour coordonnées (3 ; 0 ; 0)
Le point E a pour coordonnées (0 ; 0 ; 2)
Le point F a pour coordonnées (0 ; 4 ; 2)
Le point G a pour coordonnées (3 ; 4 ; 2)
Le point H a pour coordonnées (3 ; 0 ; 2)