Norme d'un vecteur
Définition :
La norme d'un vecteur est la longeur AB. On note
=
= AB
Propriétés :
• Dans un
repère orthonormé, si
a pour coordonnées (
x;
y), alors
=
• Quel que soit le nombre réel 𝛌 et le vecteur
,
= |𝛌|×
.
•
= 0 si et seulement si
=
.
Définition du produit scalaire
Définition :
Le
produit scalaire de deux vecteurs
et
est le
nombre réel noté
défini par :
Autre expression :
Exemple :
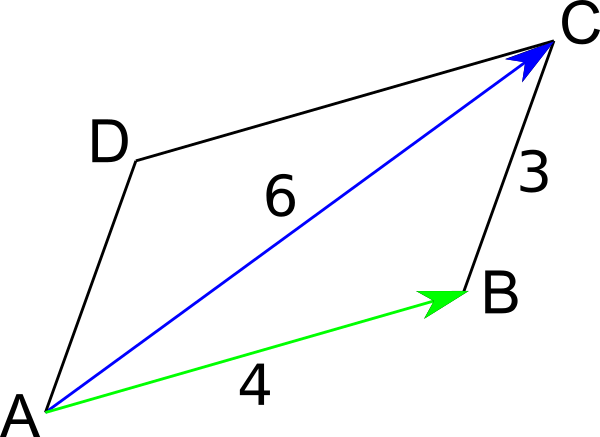
ABCD est un parallélogramme tel que AB = 4, BC = 3 et AC = 6.
Calculer
.
(d'après la
relation de Chasles)
Donc :
Si
et
sont deux vecteurs de coordonnées respectives (
x;
y) et (
x';
y') dans un
repère orthonormé, alors :
Exemple :
Dans un repère orthonormé, on considère les vecteurs
(3;-2) et
(-7;6). Calculer
.
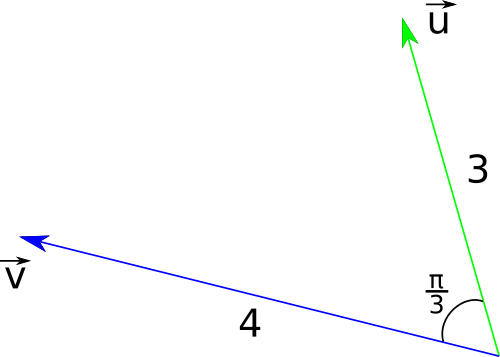
Expression avec les normes et un angle :
Pour tous vecteurs
et
distincts du vecteur nul :
Exemple :
Produit scalaire et orthogonalité
Définition :
Dire que deux vecteurs non nuls
=
et
=
sont
orthogonaux signifie que les droites (AB) et (CD) sont perpendiculaires.
Le vecteur nul
est orthogonal à tout vecteur.
Propriété :
Deux vecteurs
et
sont
orthogonaux si et seulement si
.
Exemple :
Dans un repère orthonormé, on considère les points A(-1;-2), B(2;3), C(7;-4) et D(-3;2). Montrer que les droites (AB) et (CD) sont perpendiculaires.
, donc
, donc
, donc les vecteurs
et
sont orthogonaux, donc les droites (AB) et (CD) sont perpendiculaires.
Propriétés du produit scalaire
Règles de calcul :
Pour tous vecteurs
,
et
et tout nombre réel
𝛌.
•
•
•
Produit scalaire de deux vecteurs colinéaires :
Soient
et
deux
vecteurs colinéaires.
• Si et sont de même sens, alors .
• Si et sont de sens contraire, alors .
Exemple :
Sur la droite ci-dessous, chaque graduation représente une unité.
•
•
Identités remarquables :
Quels que soient les vecteurs
et
:
• .
• .
• .
Produit scalaire et projection orthogonale
Définition :
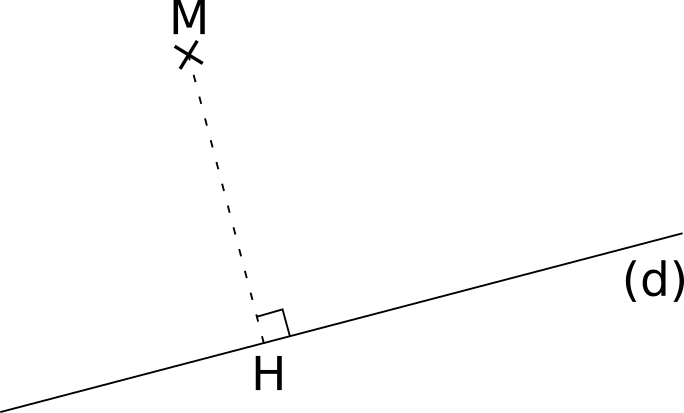
Soit M un point et (d) une droite du plan. Le
projeté orthogonal du point M sur la droite (d) est le point d'intersection H de la droite (d) et de la
perpendiculaire à M passant par (d).
Propriété :
Soient
et
deux vecteurs distincts non nuls tels que
=
et
=
, alors :
où H est le projeté orthogonal du point B sur la droite (OA).
Exemple 1 :
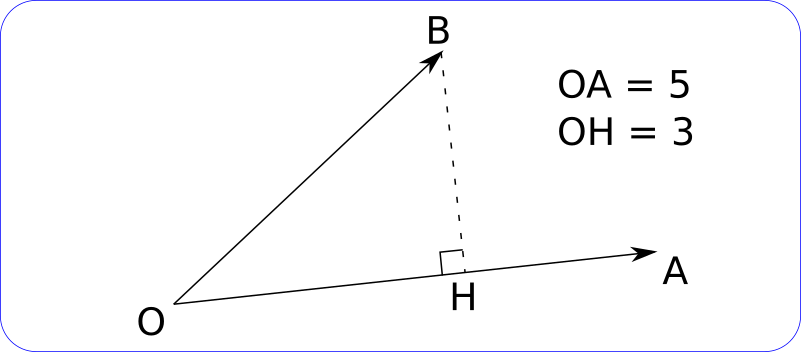
,
or
et
sont colinéaires et de même sens, donc :
, d'où
Exemple 2 :
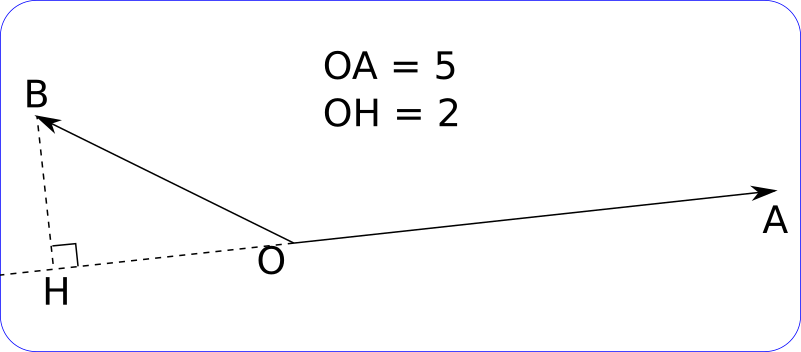
or
et
sont colinéaires et de sens contraires, donc :
, d'où