Expérience aléatoire :
Définition :
Une
expérience aléatoire est une expérience dont le résultat est
incertain.
Exemples :
| Expérience 1 |
Expérience 2 |
Expérience 3 |
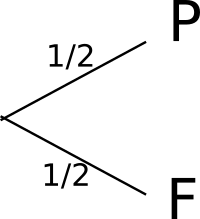
« Je lance une pièce de monnaie et je regarde la face supérieure »
 |
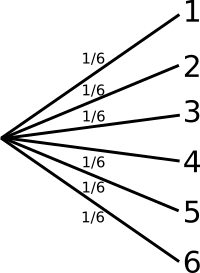
« Je lance un dé non truqué et je regarde le nombre de points sur la face supérieure »
 |
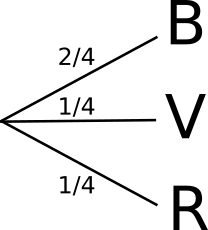
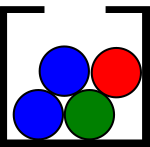
« je tire une boule dans une urne contenant 2 boules bleues 1 boule rouge et 1 boule verte et je regarde la couleur »
 |
Issue :
Chacun des résultats possibles d'une expérience aléatoire est une
issue.
Exemples :
| La pièce |
Le dé |
L'urne |
| Les issues sont Pile et Face : {P;F} |
Les issues sont les nombres entiers compris entre 1 et 6 : {1;2;3;4;5;6} |
Les issues sont Bleu, Rouge et Vert : {B;R;V} |
Événement :
Un événement est défini par une condition conduisant à zéro, une ou plusieurs issues.
Exemples :
| La pièce |
Le dé |
L'urne |
| A = « Obtenir pile » |
B = « Obtenir un nombre pair » |
C = « Obtenir une boule rouge » |
Remarques :
• un événement constitué de toutes les issues est appelé événement
certain.
• un événement constitué d'aucune issue est appelé événement
impossible.
• un événement constitué d'une seule issue est un événement
élémentaire.
Probabilité :
Définition :
La
probabilité d'un événement est un nombre compris entre 0 et 1, qui représente la chance que l'événement se réalise. Par exemple, si un événement a une chance sur 3 de se réaliser, la probabilité de cet événement est égale à 1/3. Si A est un événement, on note p(A) sa probabilité.
Exemples :
| La pièce |
Le dé |
L'urne |
A = « Obtenir pile »
p(A) = 1/2 |
B = « Obtenir un nombre pair »
p(B) = 3/6 = 1/2 |
C = « Obtenir une boule rouge »
p(C) = 1/4 |
Remarques :
• La probabilité de l'événement
certain est égale à 1.
• La probabilité d'un événement
impossible est égale à 0.
• Lorsqu'on répète une expérience aléatoire un très grand nombre de fois la fréquence de réalisation de cet événement devient proche de sa probabilité, c'est la
loi des grands nombres.
Équiprobabilité :
Lorsque tous les événements élémentaires ont la même probabilité d'être réalisés, on dit qu'il y a
équiprobabilité. Dans ce cas, la probabilité d'un événement A est égale au quotient du nombre d'issues favorables à cet événement par le nombre total d'issues de l'expérience aléatoire.
Exemples :
On tire une carte dans un jeu de 32 cartes, et on s'intéresse à la probabilité de tirer un AS. On note A l'événement : « Tirer un as ». Chaque carte a la même probabilité d'être choisie, nous sommes bien dans une situation d'équiprobabilité. Il y a 4 As dans le jeu donc :
p(A)=
Arbre des possibles :
Pour représenter les issues d'une expérience aléatoire et leur probabilité, on peut utiliser un
arbre.
Exemples :
a) Expériences simples :
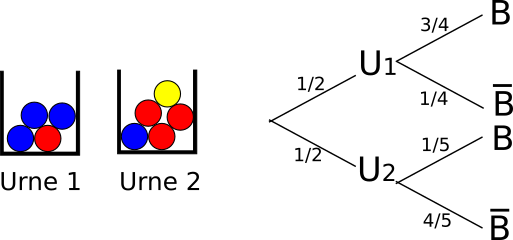
b) Expérience à deux épreuves:
On choisit une urne au hasard puis on tire une boule de cette urne. On s'intéresse à l'évènement « obtenir une boule bleue »
Propriété :
Sur un arbre, la probabilité du résultat (de l'issue) est égale au produit des probabilités rencontrées le long du chemin pour y parvenir.
Dans l'exemple précédent:
• la probabilité de choisir l'urne 1 et de tirer une boule bleue est :
P(U1,B) =
• la probabilité de choisir l'urne 2 et de tirer une boule bleue est :
P(U2,B) =
• finalement, la probabilité de choisir tirer une boule bleue est :
P(B) = p(U1,B) + p(U2,B) =