Définition :
Soit f une fonction définie sur une partie D de ℝ symétrique par rapport à 0 (exemples : [-3;3] , ]-10;10[ , ]-∞ ; +∞[ , ...).
• La fonction f est paire si : pour tout x ∈ D, f(-x) = f(x).
• La fonction f est impaire si : pour tout x ∈ D, f(-x) = -f(x).

Exemples :

1) Soit f la fonction définie sur ℝ par f(x) = x² + 2.
f(-x) = (-x)² + 2 = x² + 2 = f(x) donc f est une fonction paire.

2) Soit f la fonction définie sur ℝ par f(x) = x³ + x.
f(-x) = (-x)³ + (-x) = -x³ - x = -(x³ + x) = -f(x) donc f est une fonction impaire.

3) Soit f la fonction définie sur ℝ par f(x) = 2x² + x.
f(-x) = 2(-x)² + (-x) = 2x² - x . f(-x) ≠ f(x) et f(-x) ≠ -f(x) donc f n'est ni une fonction paire, ni une fonction impaire.

Interprétation graphique :

• Dans un repère orthogonal, la courbe représentative d'une fonction paire admet l'axe des ordonnées comme axe de symétrie.

Exemple 1 : Fonction PAIRE

La courbe C_f représente la fonction f définie sur ℝ par f(x) = $\frac{x^4}{\mathrm{32}}+x^2-3$ . f est une fonction paire, C_f est symétrique par rapport à l'axe des ordonnées.

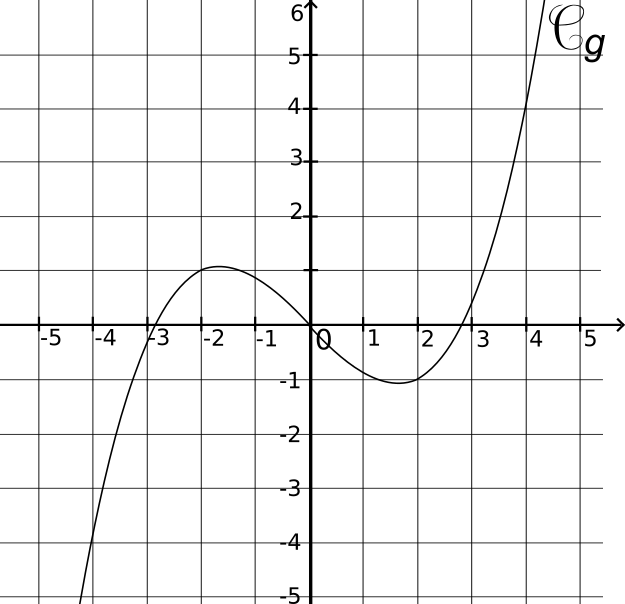
• Dans un repère orthogonal, la courbe représentative d'une fonction impaire admet l'origine du repère comme centre de symétrie.

Exemple 2 : Fonction IMPAIRE

La courbe C_g représente la fonction g définie sur ℝ par g(x) = $\frac{x^3}{8}-x$ . g est une fonction impaire, C_g est symétrique par rapport à l'origine du repère.