Cours : Loi binomiale

Epreuve et schéma de Bernoulli

Epreuve de Bernoulli :

Définition : Une épreuve de Bernoulli est une expérience aléatoire qui comporte exactement deux issues : succès(S) ou échec(S) .

Exemples :

Exemple 1	Exemple 2	Exemple 3
« Je lance une pièce de monnaie et je regarde la face supérieure » Succès : « Pile » Echec : « Face »	« Je lance un dé et je regarde le nombre de points sur la face supérieure » Succès : « obtenir 6 » Echec : « obtenir 1,2,3,4 ou 5 »	« je tire une boule dans une urne contenant 2 boules jaunes et 8 boules noires et je regarde la couleur» Succès : « jaune » Echec : « noire »

Loi de Bernoulli :

Définition : Une loi de Bernoulli est une loi de probabilité définie sur l'ensemble E={S,S} des issues d'une épreuve de Bernoulli.
Si P(S) = p, alors P( S) = 1 - p. La loi de Bernoulli de paramètre p est alors donnée par le tableau ci-dessous :

Issue	S	S
Probabilité	p	1-p

Exemples :

Exemple 1

Exemple 2

On lance une pièce de monnaie équilibrée. On appelle succès l'issue Pile et échec l'issue Face.
La loi associée à cette épreuve est la loi de Bernoulli de paramètre

\frac{1}{2}

Issue	S	S
Probabilité	$\frac{1}{2}$	$\frac{1}{2}$

On lance un dé équilibré. On appelle succès S = « Obtenir un multiple de 3 » et échec S = « Ne pas obtenir un multiple de 3 » . P(S) =

\frac{1}{3}

.
La loi associée à cette épreuve est la loi de Bernoulli de paramètre

\frac{1}{3}

Issue	S	S
Probabilité	$\frac{1}{3}$	$\frac{2}{3}$

Schéma de Bernoulli :

Définition : Un schéma de Bernoulli est une répétition d'épreuves de Bernoulli identiques et indépendantes.

Exemple :

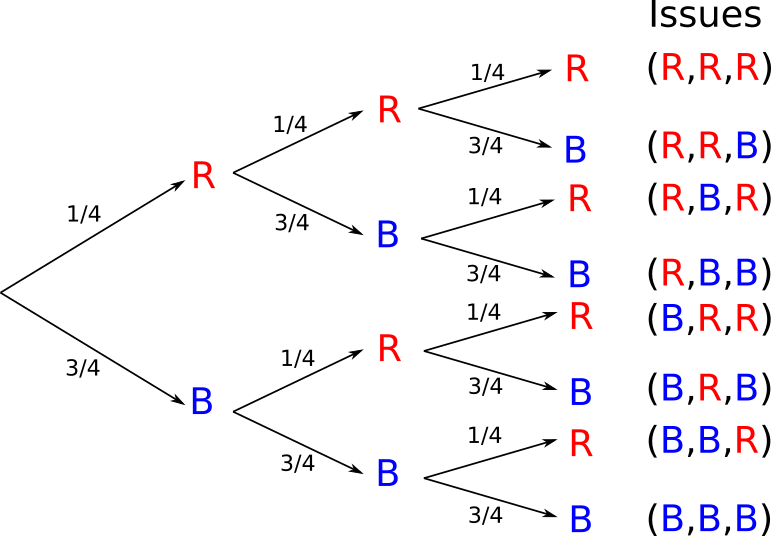
Un sac contient trois billes bleues et une bille rouge. On tire au hasard une bille de ce sac, on regarde la couleur de la bille puis on la remet dans le sac. Si la bille est rouge, c'est un succès. On considère le schéma de Bernoulli qui consiste à repéter trois fois cette expérience. On peut représenter ce schéma à l'aide de l'arbre ci-dessous.

ATTENTION ! Si on ne remet pas la bille dans le sac, il ne s'agit pas d'un schéma de Bernoulli car les expériences ne sont plus identiques ni indépendantes. La probabilité de tirer une boule bleue ne serait pas la même pour chaque tirage.

La loi binomiale

La loi binomiale :

Définition : On considère un schéma de Bernoulli qui consiste à répéter n épreuves de Bernoulli de paramètre p. Soit X la variable aléatoire qui associe le nombre de succès à chaque issue de ce schéma. La loi de probabilité de X est appelée loi binomiale de paramètres n et p ( on dira que X suit la loi binomiale de paramètres n et p et on notera X ↪ B rond

(n,p) ).

Exemple :
Reprenons l'exemple précédent du sac de billes (1 rouge et 3 bleues) et notons X la variable aléatoire égale au nombre de boules rouges tirées. Puisqu'on effectue trois tirages, X peut prendre comme valeur 0, 1, 2 ou 3. X suit la loi binomiale de paramètres 3 et $\frac{1}{3}$ ( X ↪ B rond

(3,

\frac{1}{3}

) )

P(X=0)

P(X=0) est égale à la probabilité de n'avoir aucune boule rouge

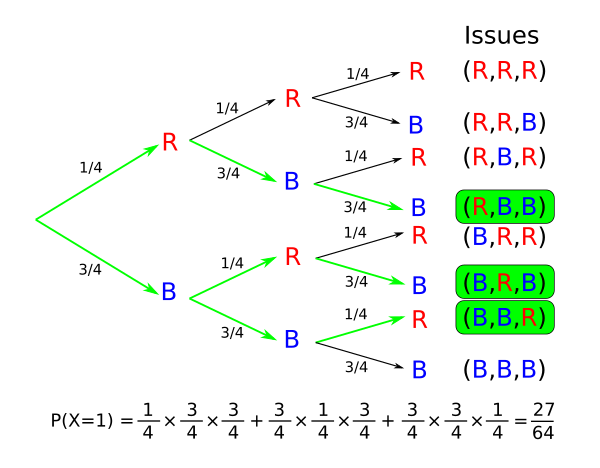
P(X=1)

P(X=1) est égale à la probabilité d'avoir 1 boule rouge

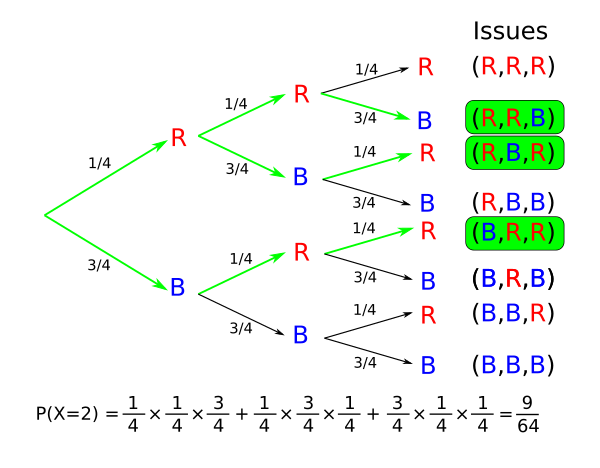
P(X=2)

P(X=2) est égale à la probabilité d'avoir 2 boules rouges

P(X=3)

P(X=3) est égale à la probabilité d'avoir 3 boules rouges

La loi de probabilité de X est donnée par le tableau suivant :

k	0	1	2	3
P(X=k)	$\frac{27}{64}$	$\frac{27}{64}$	$\frac{9}{64}$	$\frac{1}{64}$

On peut vérifier que P(X=0) + P(X=1) + P(X=2) + P(X=3) = 1

Les coefficients binomiaux :

Définition : On considère un schéma de Bernoulli de paramètres n et p représenté par un arbre. Quel que soit le nombre entier k compris entre 0 et n, le nombre de chemins réalisant k succès parmi les n épreuves est noté

(\begin{matrix} n \\ k \end{matrix})

(on lit « k parmi n »). Ces nombres sont appelés les coefficients binomiaux.

Exemple :
En utilisant l'arbre de l'exemple précédent, on trouve :

(\begin{matrix} 3 \\ 0 \end{matrix}) = 1

(\begin{matrix} 3 \\ 1 \end{matrix}) = 3

(\begin{matrix} 3 \\ 2 \end{matrix}) = 3

(\begin{matrix} 3 \\ 3 \end{matrix}) = 1

Théorème : Soit X une variable aléatoire qui suit une loi binomiale de paramètres n et p. Quel que soit le nombre entier k tel que 0≤k≤n, on a :

P(X=k) = (\begin{matrix} n \\ k \end{matrix}) p^{k} {(1 - p)}^{n - k}

Propriétés : Pour tous entiers n et k tels que n ≥ 1 et 0≤k≤n, on a :

(\begin{matrix} n \\ 0 \end{matrix}) = 1

(\begin{matrix} n \\ n \end{matrix}) = 1

(\begin{matrix} n \\ k \end{matrix}) = (\begin{matrix} n \\ n - k \end{matrix})

Triangle de Pascal : Pour tous entiers n et k tels que n ≥ 1 et 0≤k≤n-1, on a :

(\begin{matrix} n + 1 \\ k + 1 \end{matrix}) = (\begin{matrix} n \\ k \end{matrix}) + (\begin{matrix} n \\ k + 1 \end{matrix})

On peut calculer les coefficients binomiaux en utilisant le triangle de Pascal représenté ci contre. Chaque nombre du tableau est obtenu en additionnant le nombre situé juste au-dessus et celui situé à gauche de celui-ci (voir animation)

Espérance, variance, écart type :

Propriété : Si X est une variable aléatoire qui suit une loi binomiale de paramètre n et p, alors :

• E(X) = np

• V(X) = np(1-p)

• σ(X)=

\sqrt{n p (1 - p)}