Limite finie d'une fonction en l'infini
Définition :
Soit l un nombre réel.
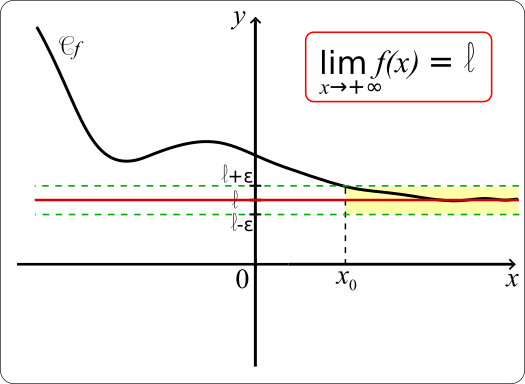
• Une fonction f a pour limite l en +∞ si tout intervalle ouvert contenant l contient toutes les valeurs f(x) dès que x est assez grand.
On note alors
l
Autrement dit, pour tout nombre réel ε>0, il existe un nombre réel x0 tel que pour tout x>x0, f(x) ∈ ]l-ɛ;l+ɛ[
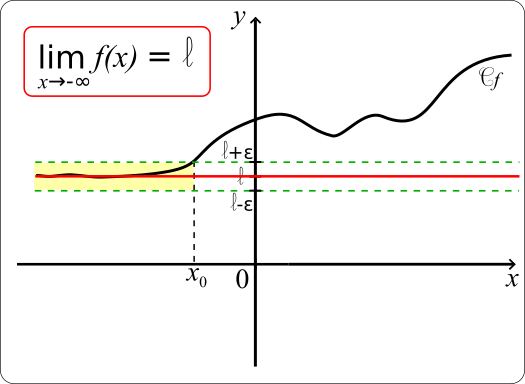
• Une fonction f a pour limite l en -∞ si tout intervalle ouvert contenant l, contient toutes les valeurs f(x) dès que x est négatif et assez grand en valeur absolue.
On note alors
l
Autrement dit, pour tout nombre réel ε>0, il existe un nombre réel x0 tel que pour tout x<x0, f(x) ∈ ]l-ɛ;l+ɛ[
Définition :
Si une fonction
f a pour
limite l en +∞ (respectivement en -∞), alors la droite d'équation
y=
l est une
asymptote horizontale à la courbe représentative de
f en +∞ (respectivement en -∞).
Exemple :
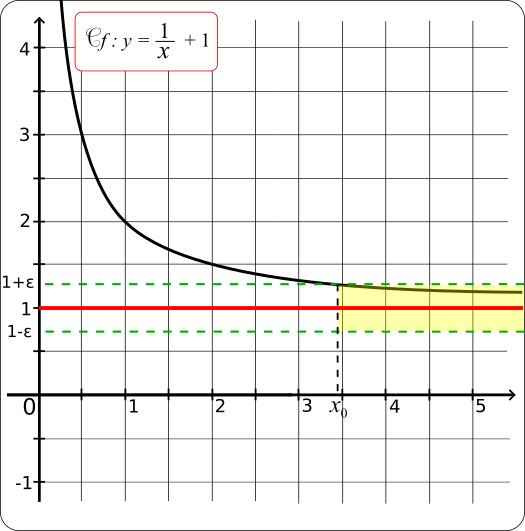
Soit f la fonction définie sur ]0;+∞[ par .
Montrons que
Soit ε>0. Posons x0=.
Quel que soit x>x0 :
, car la fonction inverse est décroissante sur ]0;+∞[
De plus, , car x>0, donc f(x)∈ ]1-ɛ;1+ɛ[.
Donc
La droite d'équation y=1 est donc asymptote horizontale à la courbe représentative de f en +∞
Limite finie en l'infinie de fonctions usuelles :
,
,
, avec n un entier strictement positif
,
, avec n un entier strictement positif,
Limite infinie d'une fonction en l'infini
Définitions :
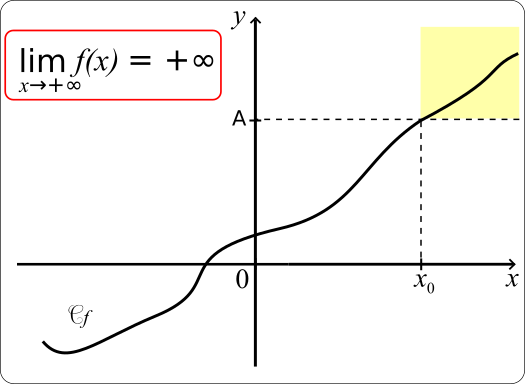
• Une fonction f a pour limite +∞ en +∞ si tout intervalle ouvert de la forme ]A;+∞[, où A est un nombre réel, contient toutes les valeurs f(x) dès que x est assez grand.
On note alors
+∞
Autrement dit, pour tout nombre réel A>0, il existe un nombre réel x0 tel que pour tout x>x0, f(x) > A
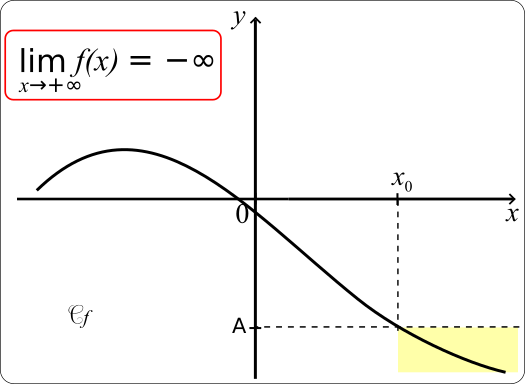
• Une fonction f a pour limite -∞ en +∞ si tout intervalle ouvert de la forme ]-∞;A[, où A est un nombre réel, contient toutes les valeurs f(x) dès que x est assez grand .
On note alors
-∞
Autrement dit, pour tout nombre réel A<0, il existe un nombre réel x0 tel que pour tout x>x0, f(x) < A
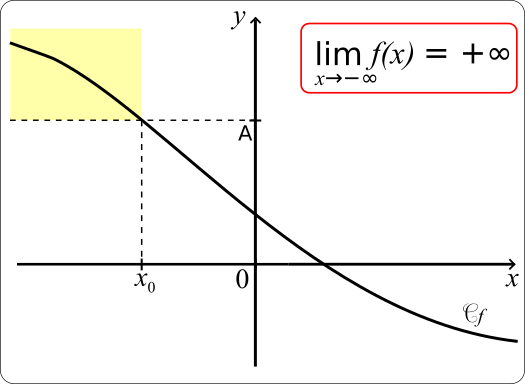
• Une fonction f a pour limite +∞ en -∞ si tout intervalle ouvert de la forme ]A;+∞[, où A est un nombre réel, contient toutes les valeurs f(x) dès que x est négatif et assez grand en valeur absolue.
On note alors
+∞
Autrement dit, pour tout nombre réel A>0, il existe un nombre réel x0 tel que pour tout x<x0, f(x) > A
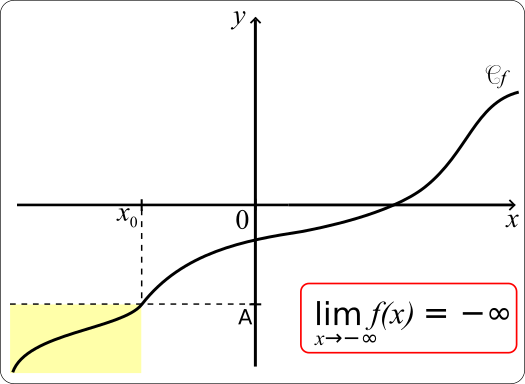
• Une fonction f a pour limite -∞ en -∞ si tout intervalle ouvert de la forme ]-∞;A[, où A est un nombre réel, contient toutes les valeurs f(x) dès que x est négatif et assez grand en valeur absolue.
On note alors
-∞
Autrement dit, pour tout nombre réel A<0, il existe un nombre réel x0 tel que pour tout x<x0, f(x) < A
Limite infinie en l'infinie de fonctions usuelles :
,
,
,
, avec n un entier strictement positif
,
, si n est un entier
pair strictement positif
,
, si n est un entier
impair strictement positif
Limite infinie d'une fonction en un point
Définition :
Soit
f une fonction et
a un nombre réel.
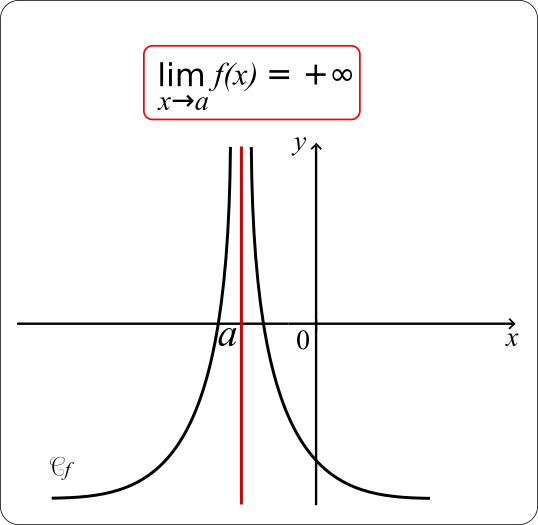
• Une fonction f a pour limite +∞ en a si tout intervalle ouvert de la forme ]A;+∞[, où A est un nombre réel, contient toutes les valeurs f(x) dès que x est assez proche de a.
On note alors
+∞
Autrement dit, pour tout nombre réel A>0, il existe un nombre réel ε>0 tel que pour tout x∈]a-ε; a+ε[ (avec x≠a), f(x) > A
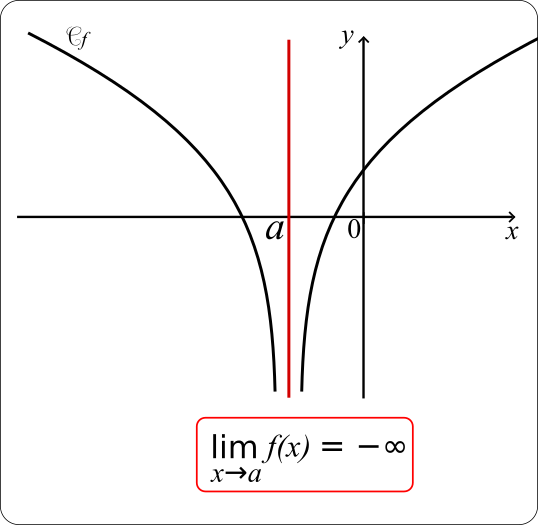
• Une fonction f a pour limite -∞ en a si tout intervalle ouvert de la forme ]-∞;A[, où A est un nombre réel, contient toutes les valeurs f(x) dès que x est assez proche de a.
On note alors
-∞
Autrement dit, pour tout nombre réel A<0, il existe un nombre réel ε>0 tel que pour tout x∈]a-ε; a+ε[ (avec x≠a), f(x) < A
Remarques :
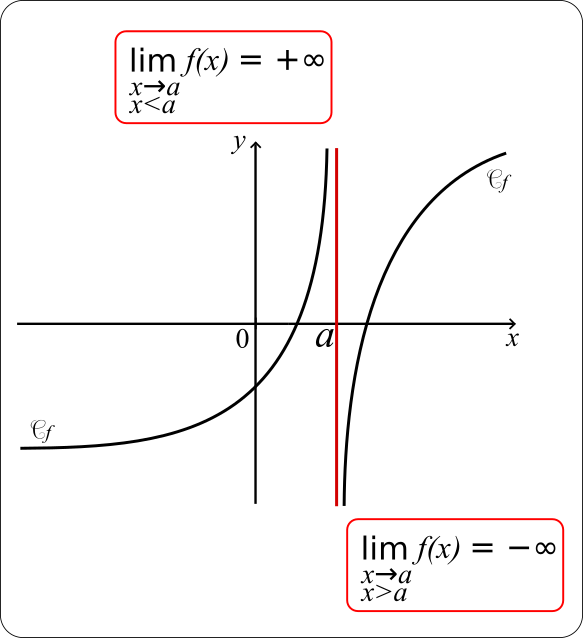
• On appelle limite à droite de f en a, la limite de f(x) lorsque x tend vers a avec x>a.
On la note
• On appelle limite à gauche de f en a, la limite de f(x) lorsque x tend vers a avec x<a.
On la note
Exemple :
Soit
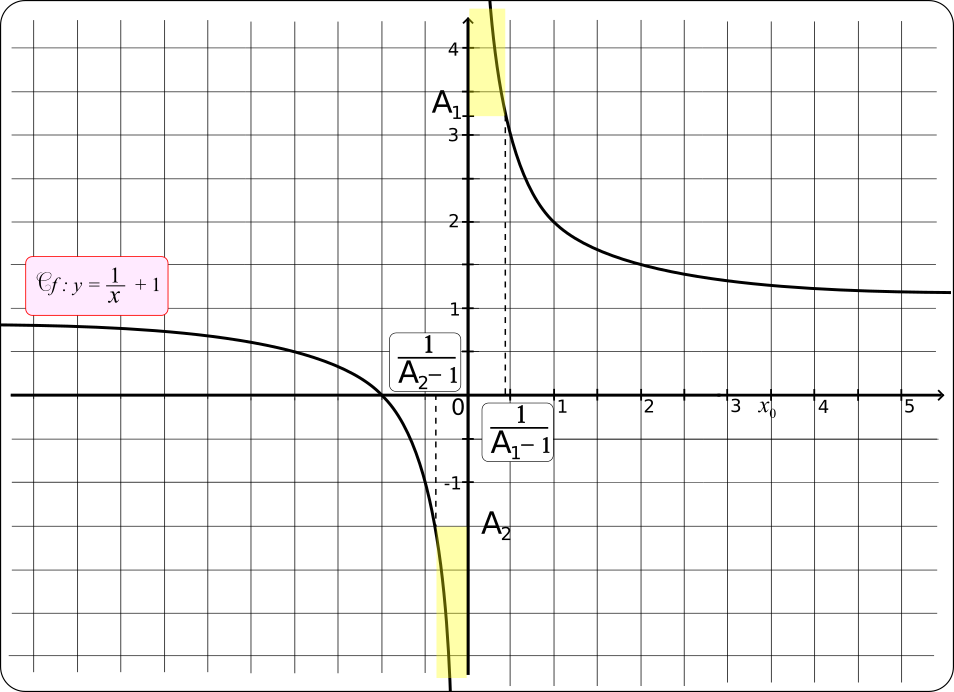
f la fonction définie sur ]-∞;0[∪]0;+∞[ par
.
1) Montrons que
Soit A1>0. Posons x0 =.
Quel que soit x∈]0;x0[ :
donc
Donc f(x) > A1 .
Donc
2) Montrons que
Soit A2<0. Posons x0 =.
Quel que soit x∈]x0;0[ :
donc
Donc f(x) < A2 .
Donc
La droite d'équation
x=0 est donc asymptote verticale à la courbe représentative de
f
Limites et opérations
Soit
f et
g deux fonctions. Soit
l et
l' deux nombres réels. Le symbole ±∞ signifie «soit +∞ soit −∞».
a désigne un nombre réel ou +∞ ou -∞.
Le sigle F.I signifie «Forme Indéterminée», c'est à dire qu'on ne peut pas conclure.
Limite d'une somme :
|
| l | l | l | +∞ | +∞ | −∞ |
|
| l' | +∞ | −∞ | +∞ | −∞ | −∞ |
|
| l+l' | +∞ | −∞ | +∞ | F.I. | −∞ |
Limite d'un produit :
| | l | l>0 | l>0 | l<0 | l<0 | ±∞ | 0 |
| | l' | +∞ | −∞ | +∞ | −∞ | ±∞ | ±∞ |
| | l×l' | +∞ | −∞ | −∞ | +∞ | ±∞ | F.I. |
Limite d'un quotient :
| | l | l | ±∞ | ±∞ | l≠0 | ±∞ | 0 |
| | l'≠0 | ±∞ | l'≠0 | ±∞ | 0+ ou 0− | 0+ ou 0− | 0 |
|
|
|
0 | ±∞ | F.I. | ±∞ | ±∞ | F.I. |
Exemple :
Soit
f:
x ↦
définie sur ℝ*. Calculer
Solution :
•
.
•
.
Par produit,
Limite d'une fonction composée
Définition :
Soit
f une fonction définie sur E et à valeurs dans F, et soit
g une fonction définie sur F.
La composée de f suivie de g est la fonction notée
g ○ f définie pour tout
x de E par
g ○ f(x)=g(f(x))
Remarque : l'ordre des fonctions est important,
g ○ f et
f ○ g ne sont en général pas les mêmes fonctions.
Exemple :
Soit
f et
g deux fonctions définies sur ℝ par
f(x)=
x² et
g(x)=
x+3.
• Pour tout
x ∈ ℝ,
g ○ f(x) =
g(f(x)) =
g(x²) =
x²+3
• Pour tout
x ∈ ℝ,
f ○ g(x) =
f(g(x)) =
f(x+3) =
(x+3)²
Théorème :
Soit
f et
g deux fonctions. Soient
a,
b et
c trois réels ou +∞ ou -∞.
Si
et
, alors
.
Exemple :
Calculer
Soit
f définie sur ℝ\{-2} par
et
g définie sur ℝ par
.
Donc, par composition,
Limites et comparaison
Théorème de comparaison :
Soient
a,
b, et
c trois nombres réels.
Soit
f et
g deux fonctions telles que
f(x)≤
g(x) sur un intervalle ]
a;+∞[ de ℝ.
• Si , alors
• Si , alors
Soit
f et
g deux fonctions telles que
f(x)≤
g(x) sur un intervalle ]-∞;
a[ de ℝ.
• Si , alors
• Si , alors
Soit
f et
g deux fonctions telles que
f(x)≤
g(x) sur un intervalle ]
a;
b[ de ℝ et
c ∈ ]
a;
b[.
• Si , alors
• Si , alors
Exemple :
Soit
f la fonction définie sur ℝ par
f(x) = x + cos(x)
Pour tout nombre réel
x ∈ ℝ, -1 ≤ cos(x) ≤ 1, donc x - 1 ≤ f(x) ≤ x + 1
•
donc
•
donc
Théorème des gendarmes (encadrement) :
Soient
a,
b,
c et
l quatre nombres réels.
Soit
f,
g et
h trois fonctions telles que
f(x)≤
g(x)≤
h(x) sur un intervalle ]
a;+∞[ de ℝ.
• Si et alors
Soit
f,
g et
h trois fonctions telles que
f(x)≤
g(x)≤
h(x) sur un intervalle ]-∞;
a[ de ℝ.
• Si et alors
Soit
f,
g et
h trois fonctions telles que
f(x)≤
g(x)≤
h(x) sur un intervalle ]
a;
b[ de ℝ et
c ∈ ]
a;
b[.
• Si et alors
Exemple :
Soit
f, la fonction définie sur ]0;+∞[ par
.
Pour tout
x ∈ ℝ, -1 ≤
sin(x) ≤ 1 , donc
. Or
Donc, d'après le théorème des gendarmes,