Soit O un point du plan et
k un nombre positif. Appliquer à une figure l'
homothétie de centre O et rapport
k , consiste à multiplier par
k toutes les distances par rapport au point O. La forme de la figure est conservée mais on obtient une figure agrandie si
k > 1 et réduite si 0 < k < 1.
Si
k est un nombre négatif, la figure obtenue par l'
homothétie de centre O et rapport
k est "retournée" par rapport à l'original.
Les animations ci-dessous présentent des exemples d'homothéties de rapport positif (en haut) et un exemple d'homothétie de rapport négatif (en bas) : (clique sur le bouton pour faire défiler l'animation)
Propriétés :
Soit k >0. Effectuer une homothétie de rapport k revient à faire un
agrandissement (si k > 1) ou une
réduction (si 0 < k < 1) de coefficient k.
Lors d'une homothétie de rapport k :
• les mesures d'
angles sont conservées.
• les longueurs initiales sont multipliées par k
• les aires sont multipliées par k²
• les volumes sont multipliées par k³
Construire l'image d'un point par une homothétie :
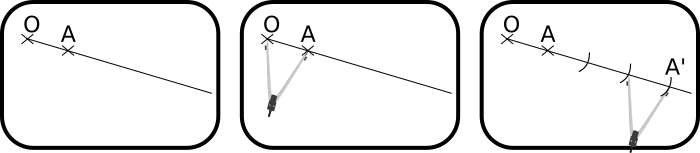
On veut construire l'image du point A par l'homothétie de centre O et de rapport 4.
Remarque : On a : OA' = 4 × OA.


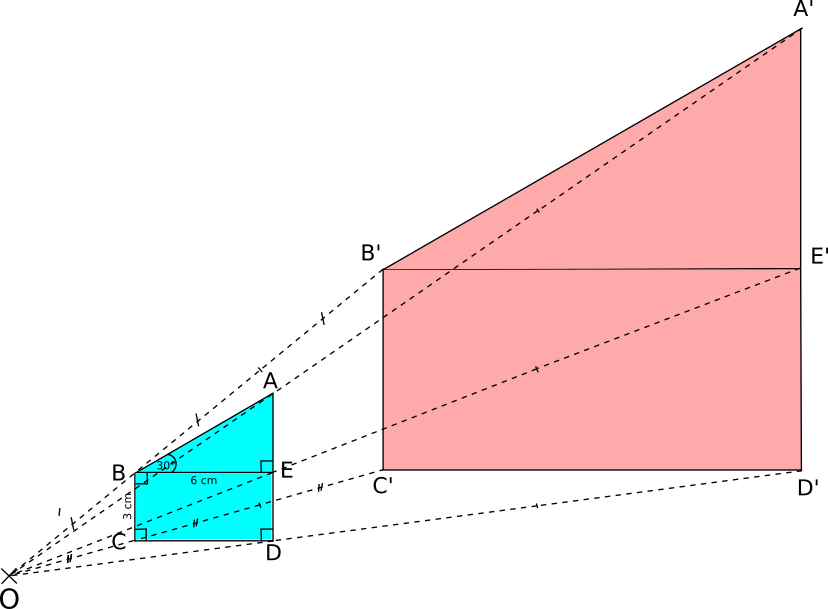




• La forme de la figure bleue est conservée.
• Les mesures d'angles de la figure rose sont les mêmes que ceux de la figure bleue : 30°
• Les longueurs de la figure rose sont égales à celles de la figure bleue multipliées par 3 : B'C' = 3 × 3 = 9 cm. B'E' = 3 × 6 = 18 cm.
• L'aire de la figure rose est égale à l'aire de la figure bleue multipliée par 9 (car 3² = 3 × 3 = 9)