Rappel : cosinus et sinus d'un nombre réel
Soit (O;
,
) un repère orthonormé et
le cercle trigonométrique de centre O.
Soit
x un nombre réel et M l'image de
x sur le cercle
(c'est à dire que M est le point du cercle
tel que (
,
) = x rad).
Le
cosinus de
x, noté
cos(x) est l'abscisse de M.
Le
sinus de
x, noté
sin(x) est l'ordonnée de M.
Valeurs remarquables de sinus et cosinus :
| x |
0 |
|
|
|
|
π |
| cos(x) |
1 |
|
|
|
0 |
-1 |
| sin(x) |
0 |
|
|
|
1 |
0 |
Démonstrations :
Soit (O; A, B) un repère orthonormé et
le
cercle trigonométrique de centre O .
sin() ; cos()
Soit M l'image de
sur
.
[OA] et [OM] sont deux rayons du cercle
, donc OA = OM = 1 et le triangle OAM est
isocèle en O. De plus (
,
)=
, donc (
,
) = (
,
)=
et le triangle AMO est
équilatéral.
Soit H le pied de la
hauteur issue de M dans le triangle AMO. Puisque AMO est équilatéral, (MH) est la
médiatrice de [OA], donc H est le milieu de [OA], donc cos(
) = OA/2 =
.
D'après le
théorème de Pythagore dans le triangle rectangle OMH :
HM²=OM²-OH²=1-
=
.
D'où sin(
)=HM=
.
sin() ; cos()
Soit M l'image de
sur
.
Soit H le point du segment [OA] tel que (MH)⊥(OA).
Dans le triangle MOH, on a (
,
)=
- (
,
) - (
,
)=
. Le triangle MOH est donc
isocèle rectangle en H. De plus [OM] est un rayon du cercle donc OM=1.
D'après le
théorème de Pythagore, OM²=OH²+MH²=2OH².
Donc OH²=
donc OH=
=
.
D'où sin(
)=cos(
)=
.
Fonction sinus
Parité :
Quel que soit le réel x,
sin(-x) = -sin(x) (voir figure ci-contre).
On dit que la fonction sinus est
impaire.
Périodicité :
Quel que soit le réel x, sin(x+2π) = sin(x). On dit que la fonction sinus est
périodique de période 2π (ou 2π-périodique).
Courbe représentative :
Sur l'animation ci-dessous, un nombre réel x varie entre -2π et 2π. Le point rouge est l'image de x sur le cercle trigonométrique. Au fur et à mesure que le point rouge parcourt le cercle trigonométrique, le point bleu trace la représentation graphique de la fonction sinus dans un repère orthogonal.
Lien entre le cercle trigonométrique et la représentation graphique de la fonction sinus
La courbe représentative de la fonction sinus est appelée une
sinusoïde.
• Courbe et parité : puisque la fonction sinus est
impaire, sa courbe représentative est symétrique par rapport à l'origine du repère.
• Courbe et périodicité : puisque la fonction sinus est
2π-périodique, sa courbe représentative dans un repère (O;
,
) est invariable par toute translation de vecteur k×2π
(avec k un entier relatif)
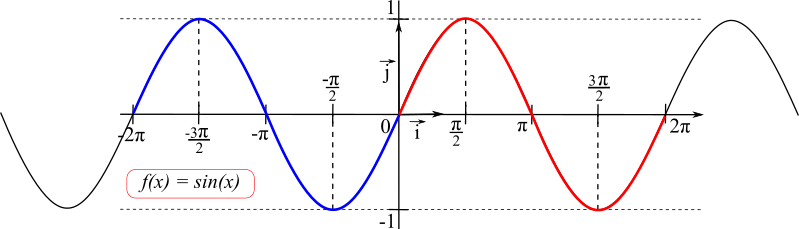
La partie de courbe rouge est obtenue en effectuant une translation de la partie de bleue de vecteur 2π
Fonction cosinus :
Parité :
Quel que soit le réel x,
cos(-x) = cos(x) (voir figure ci-contre).
On dit que la fonction cosinus est
paire.
Périodicité :
Quel que soit le réel x, cos(x+2π) = cos(x). On dit que la fonction cosinus est
périodique de période 2π (ou 2π-périodique).
Courbe représentative :
Sur l'animation ci-dessous, un nombre réel x varie entre -2π et 2π. Le point rouge est l'image de x sur le cercle trigonométrique. Au fur et à mesure que le point rouge parcourt le cercle trigonométrique, le point bleu trace la représentation graphique de la fonction cosinus dans un repère orthogonal.
Lien entre le cercle trigonométrique et la représentation graphique de la fonction cosinus
La courbe représentative de la fonction cosinus est également appelée une
sinusoïde.
• Courbe et parité : puisque la fonction cosinus est
paire, sa courbe représentative est symétrique par rapport à l'axe des abscisses.
• Courbe et périodicité : puisque la fonction sinus est
2π-périodique, sa courbe représentative dans un repère (O;
,
) est invariable par toute translation de vecteur k×2π
(avec k un entier relatif)
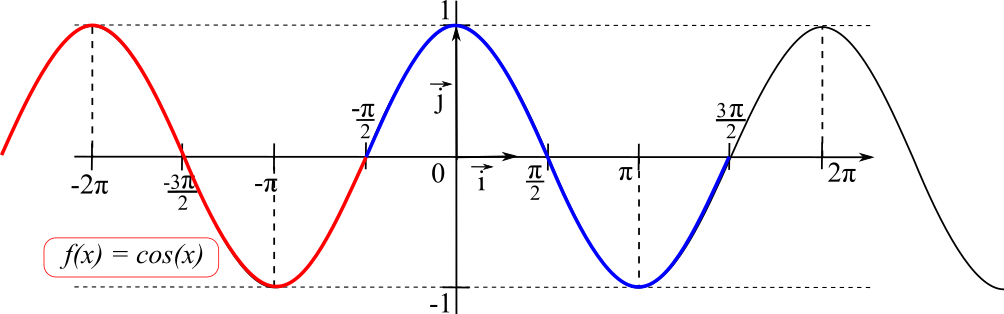
La partie de courbe rouge est obtenue en effectuant une translation de la partie de bleue de vecteur -2π
