Cours : Fonction logarithme

La fonction logarithme népérien

Définition :
• Soit a un réel strictement positif. On appelle logarithme népérien de a, l'unique solution de l'équation e^x=a. On le note ln(a).
• La fonction qui à tout réel x > 0, associe le réel ln(x) est appelée fonction logarithme népérien. C'est la fonction réciproque de la fonction exponentielle. Elle est définie sur ]0;+∞[ et est notée ln.

Preuve de l'unicité de la solution : La fonction exponentielle est continue et strictement croissante sur ℝ et

lim_{x →-∞} e^{x} = 0

lim_{x →+∞} e^{x} = +∞

. Donc d'après le théorème des valeurs intermédiaires, pour tout réel a>0, l'équation

e^{x}

= a admet une unique solution dans ℝ.

Exemple : Déterminer un ensemble de définition
Soit f la fonction définie par f(x) = ln (2x+4).
ln (2x+4) existe si et seulement si 2x+4>0, c'est à dire x>-2. L'ensemble de définition de f est donc ]-2;+∞[.

Propriétés :

• Pour tout réel x et pour tout réel y > 0, e^x=y ⇔ x=ln(y)
• ln(1) = 0 (car e⁰=1)
• ln(e) = 1 (car e¹=e)
• Pour tout réel x > 0, e^ln(x) = x
• Pour tout réel x, ln(e^x) = x

Exemples : résoudre une équation
1) Résoudre dans ℝ l'équation e^2x-5=3.
Solution : e^2x-5=3 ⇔ 2x-5 = ln(3) ⇔ 2x = ln(3)+5 ⇔ x =

\frac{ln(3)+5}{2}

2) Résoudre dans ℝ l'équation ln(2x-5)=3.
Solution : ln(2x-5) existe si et seulement si 2x-5>0, c'est à dire x>5/2.
ln(2x-5)=3⇔ 2x-5=e³⇔ 2x=e³+5⇔ x=

\frac{e^{3} + 5}{2}

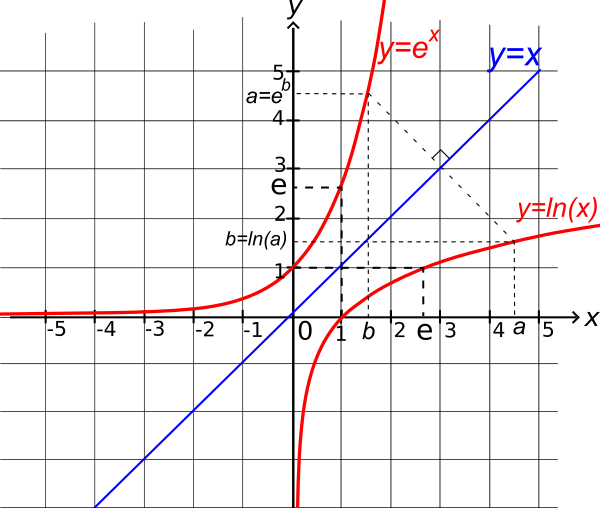
Courbes des fonction ln et exp :

Dans un repère orthonormé, les courbes réprésentatives des fonctions ln et exp sont symétriques par rapport à la droite d'équation y=x.

Propriétés algébriques

Propriété : Relation fonctionnelle
Pour tous les réels x et y strictement positifs :

ln(xy) = ln(x) + ln(y)

Propriétés
Pour tous les réels x et y strictement positifs, et pour tout entier relatif n :
•

ln(\frac{1}{x}) = - ln(x)

•

ln(\frac{x}{y}) = ln(x) - ln(y)

•

ln(x^{n}) = n ln(x)

•

ln(\sqrt{x}) = \frac{1}{2} ln(x)

Exemple :
Simplifier l'expression ln(4)+ln(2)-ln(8).
Solution : ln(4)+ln(2)-ln(8) = ln(4×2)-ln(8) = ln(8/8) = ln(1)= 0

Etude de la fonction logarithme népérien

Dérivée de la fonction ln
• La fonction logarithme népérien est continue et dérivable sur ]0;+∞[ et pour tout réel x strictement positif :

ln'(x) = \frac{1}{x}

• Soit u une fonction dérivable et strictement positive sur un intervalle I. La fonction ln(u) est dérivable sur I et :

ln'(u (x)) = \frac{u' (x)}{u (x)}

Exemple :
Soit f la fonction définie sur ]1;+∞[ par f(x) = ln(4x-4).
f'(x) =

\frac{4}{4 x - 4}

\frac{1}{x - 1}

Variations de la fonction ln
La fonction logarithme népérien est strictement croissante sur ]0;+∞[.

Limites aux bornes de la fonction ln

lim_{\underset{x >0}{x →0}} ln(x) = -∞

lim_{x →+∞} ln(x) = +∞

Courbe représentative de la fonction ln

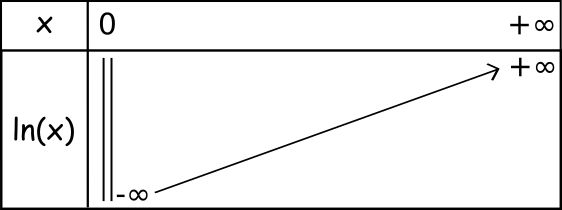Tableau de variations de la fonction logarithme népérien.

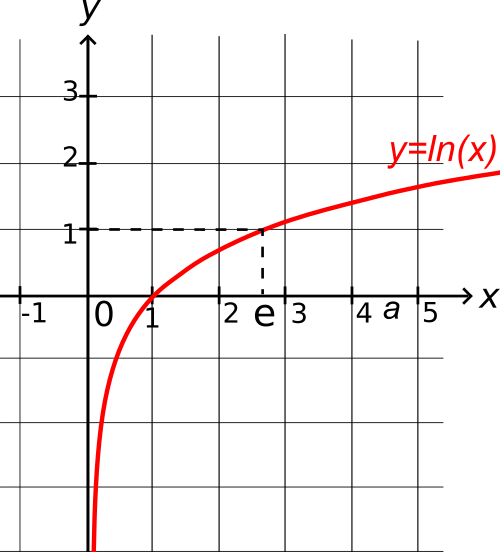Courbe représentative de la fonction logarithme népérien.

Fonction logarithme décimal

Définition
La fonction logarithme décimal, notée log, est la fonction définie sur ]0;+∞[ par :

log(x) = \frac{ln(x)}{ln(10)}

Propriétés
Pour tous les réels x et y strictement positifs, et pour tout entier relatif n :
•

log(10^{n}) = n

• la fonction log est strictement croissante sur ]0;+∞[.
• log(xy) = log(x) + log(y)
•

log(\frac{x}{y}) = log(x) - log(y)