Cours : Equations et inéquations du second degré

Equations du second degré

Définition :
Soit

f

une fonction polynôme de degré 2 de la forme :

f (x) = a x ² + b x + c

où

a

b

c

sont trois réels avec $a$ ≠ 0.
Le nombre réel Δ, égal à

b ² - 4 a c

est appelé le discriminant de

f

.

Propriété :
• Si Δ < 0 , alors l'équation

f (x) = 0

n'admet aucune solution réelle.

f

ne peut pas s'écrire sous forme factorisée.

• Si Δ = 0 , alors l'équation

f (x) = 0

admet une unique solution

x_{0} = \frac{-b}{2 a}

.
La forme factorisée de

f

est

f (x) = a (x - x_{0}) ²

• Si Δ > 0 , alors l'équation

f (x) = 0

a deux solutions

x_{1} = \frac{-b - \sqrt{Δ}}{2 a}

x_{2} = \frac{-b + \sqrt{Δ}}{2 a}

.
La forme factorisée de

f

est

f (x) = a (x - x_{1}) (x - x_{2})

Remarques :
• Les solutions de l'équation

a x ² + b x + c = 0

sont appelées racines du trinôme

a x ² + b x + c

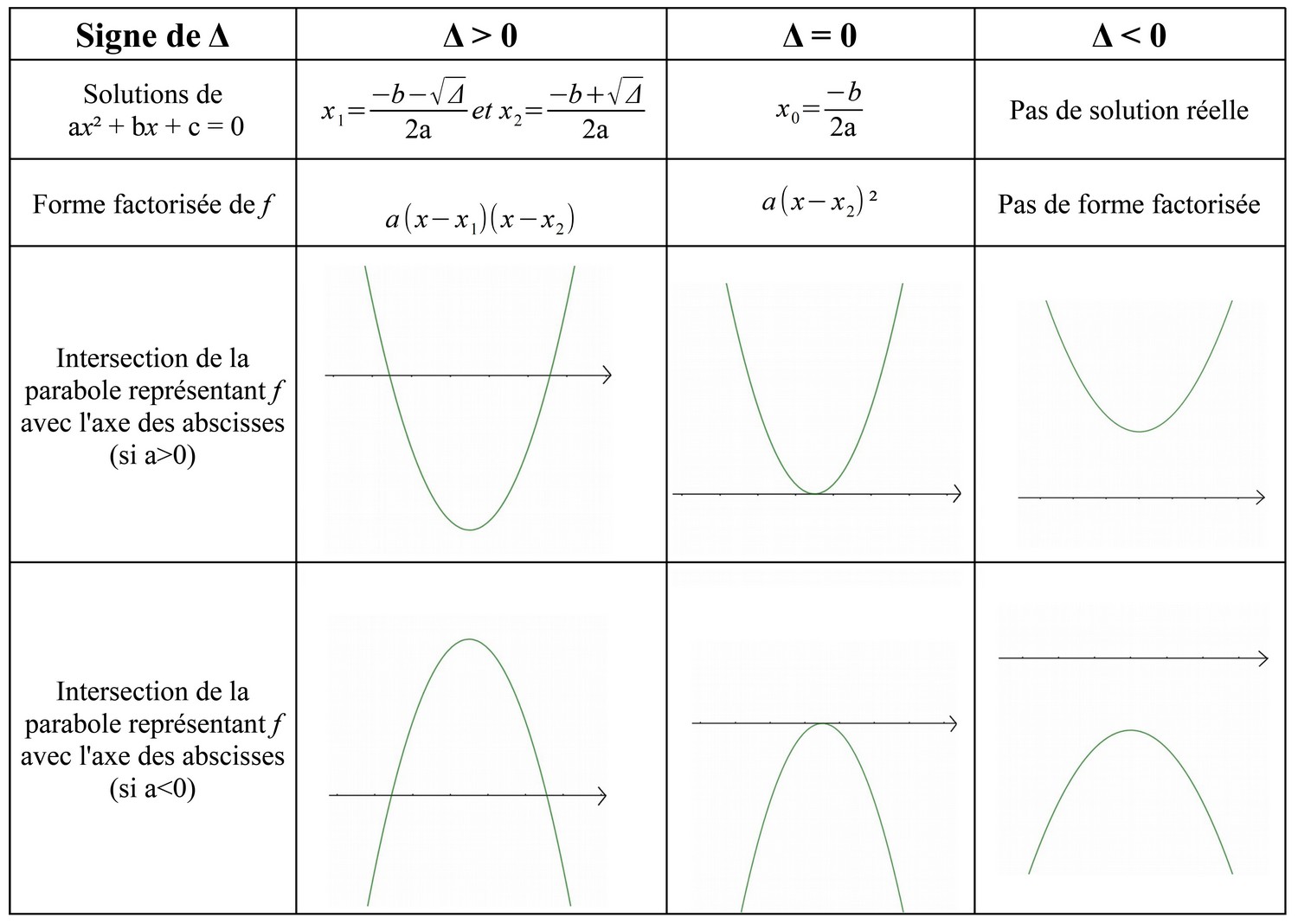
• Les solutions, lorsqu'elles existent, sont les abscisses des points d'intersection de la courbe avec l'axe des abscisse (voir tableau).

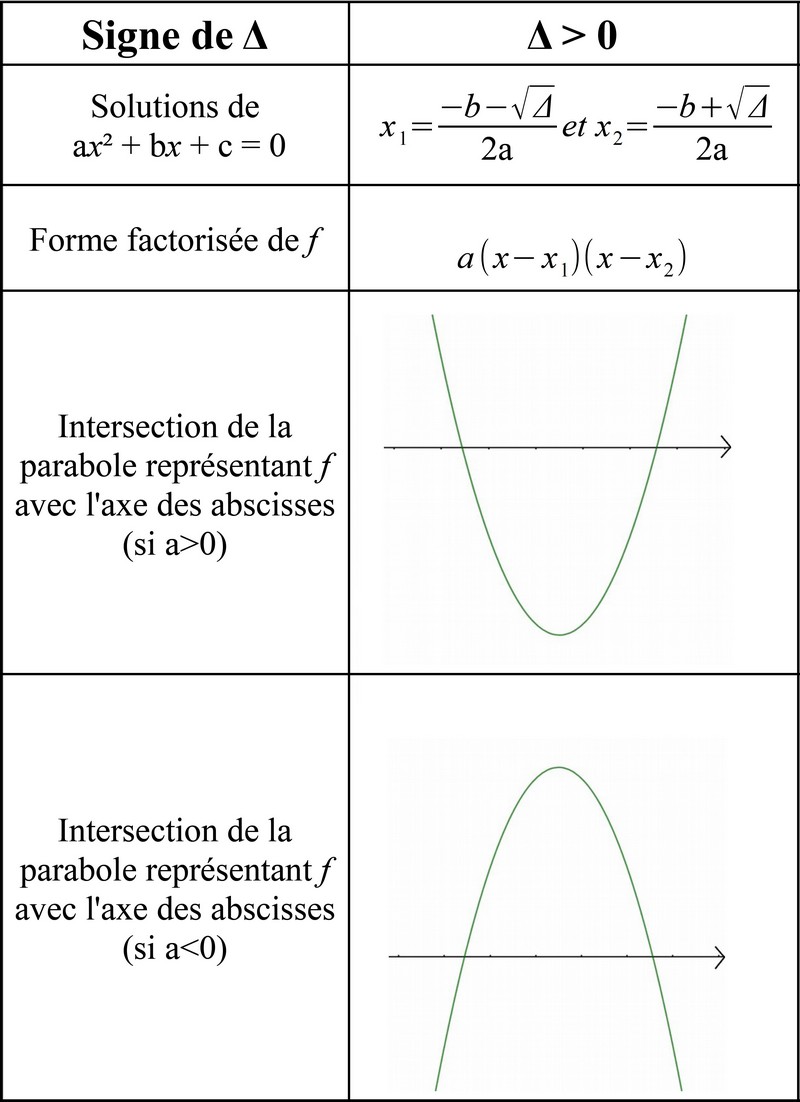
Si Δ>0

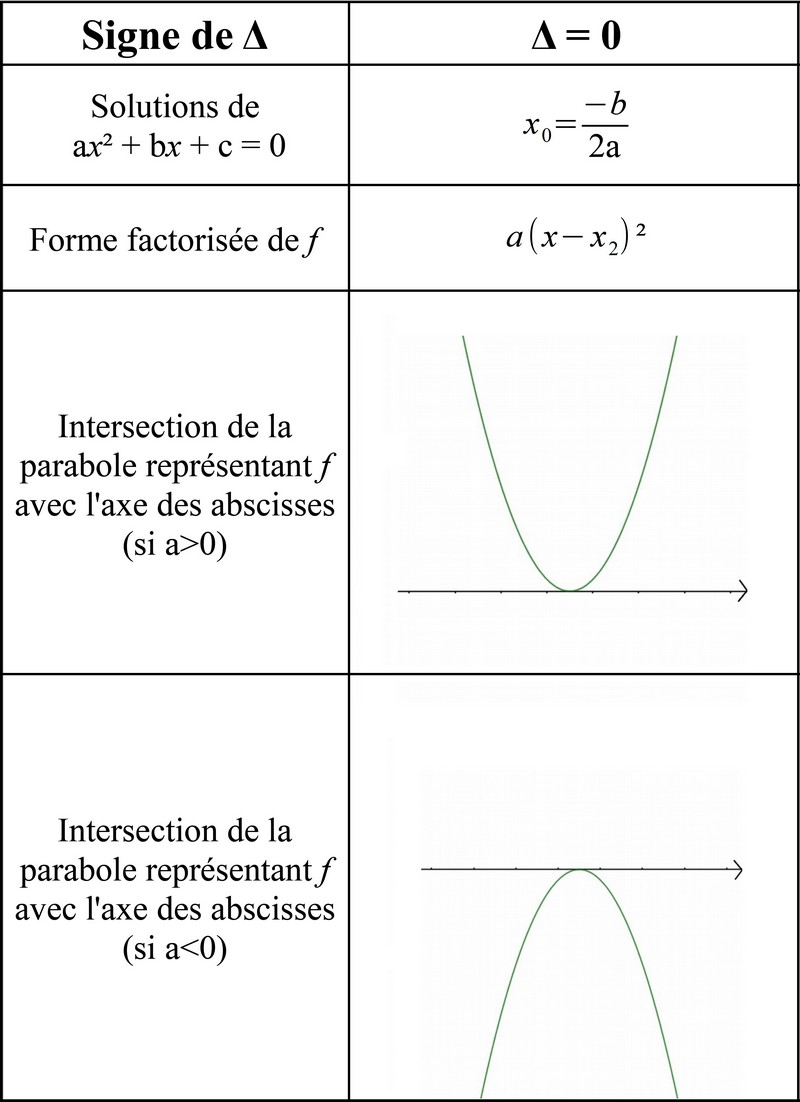
Si Δ=0

Si Δ<0

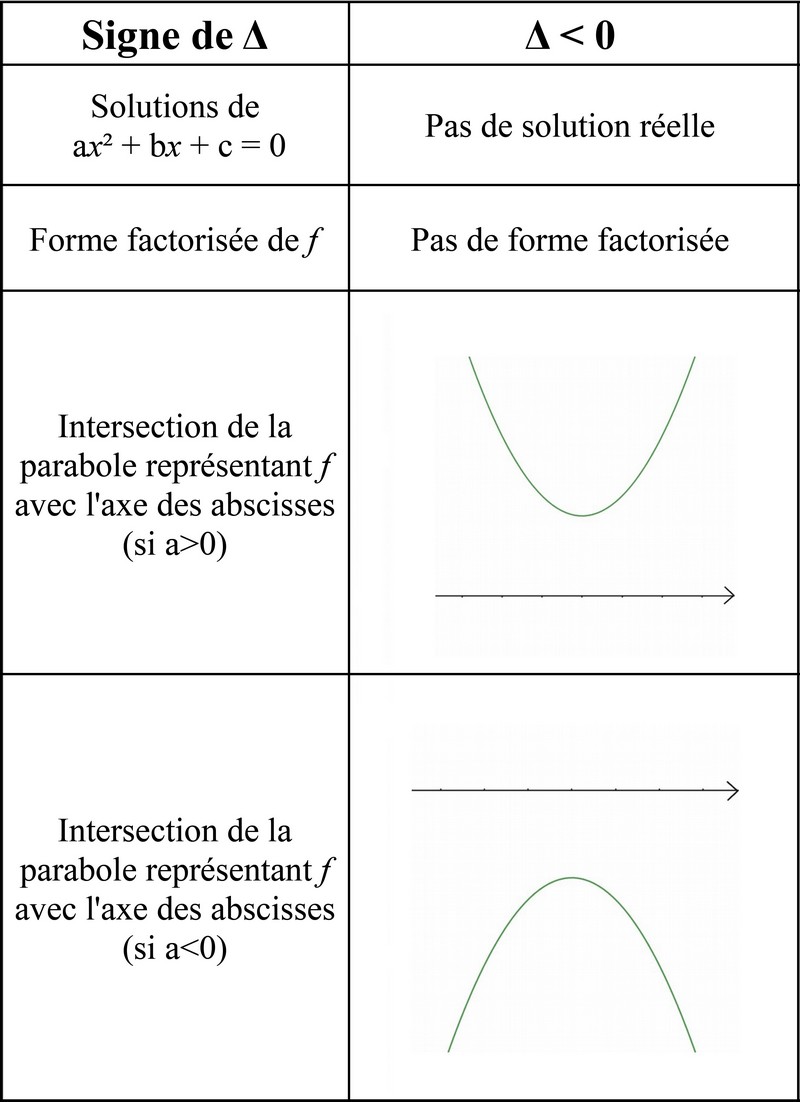
Exemples :

a) Résoudre l'équation 2x² - 5x - 3 = 0

Solution :

a = 2 , b = -5 et c = -3.
Δ = b² - 4ac
Δ = (-5)² - 4×2×(-3)
Δ = 25-(-24) = 25+24 = 49
Δ > 0, donc l'équation admet 2 solutions.

x_{1} = \frac{5 - \sqrt{49}}{2 \times 2}

x_{1} = \frac{5 - 7}{4} = \frac{-2}{4} = \frac{-1}{2}

x_{2} = \frac{5 + \sqrt{49}}{2 \times 2}

x_{2} = \frac{5 + 7}{4} = \frac{12}{4} = 3

L'équation 2x² - 5x - 3 = 0 admet deux solutions : -1/2 et 3.

2x² - 5x - 3=2(x+1/2)(x-3).

b) Résoudre l'équation 9x² - 12x + 4 = 0

Solution :

a = 9 , b = -12 et c = 4.
Δ = b² - 4ac
Δ = (-12)² - 4×9×4
Δ = 144-144 = 0
Δ = 0, donc l'équation admet 1 solution.

x_{0} = \frac{12}{2 \times 9} = \frac{12}{18} = \frac{2}{3}

L'équation 9x² - 12x + 4 = 0 admet une solution : 2/3
9x² - 12x + 4 = 9(x - 2/3)².

c) Résoudre l'équation x² + 2x + 5 = 0

Solution :

a = 1 , b = 2 et c = 5.
Δ = b² - 4ac
Δ = 2² - 4×1×5
Δ = 4 - 20 = -16
Δ < 0, donc l'équation n'admet aucune solution réelle.

Utilisation de la calculatrice :
-> Avec le mode équa des modèles casios :

1) Choisir le menu équa equation degré 2 avec casio

2) Choisir le type polynomial (f2) equation degré 2 avec casio

3) Choisir le degré 2 (f1) equation degré 2 avec casio

4) Donner les valeurs de a, b et c equation degré 2 avec casio

5) Obtenir les solutions avec solv (f1) equation degré 2 avec casio

-> Avec la fonction Solver des modèles TI :

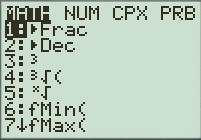
1) Choisir le menu math equation degré 2 avec casio

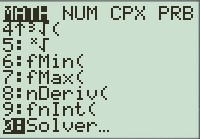
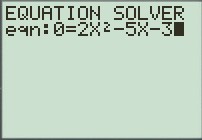
2) Choisir la fonction Solver (0) equation degré 2 avec casio

3) ax² + bx + c puis entrer equation degré 2 avec casio

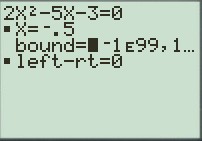
4) alpha puis entrer (résol) equation degré 2 avec casio

ATTENTION !!!
Comme on peut le constater sur cet exemple, la fonction Solve ne renvoit qu'une seule des deux solutions

Algorithme :

Pour pallier le problème de la fonction Solve(), il est possible et conseillé de programmer un algorithme qui donnera la valeur du discriminant ainsi que les racines éventuelles d'un trinôme du second degré.

Langage naturel

Saisir a,b,c
b² - 4ac -> Δ
Afficher "DELTA = ", Δ
Si (Δ>0) alors :
     $\frac{-b - \sqrt{Δ}}{2 a}$ -> $x_{1} \frac{-b + \sqrt{Δ}}{2 a} -> x_{2}$
    Afficher "Deux solutions : " x1, x2
Sinon si (Δ=0) alors :
     $\frac{-b}{2 a}$ -> $x_{0}$ .
    Afficher "Une solution : " x0
Sinon,
    Afficher "Pas de solution réelle".

Casio

"A"?→A
"B"?→B
"C"?→C
"DELTA"
B²-4AC→D

If D>0
Then "2 SOLUTIONS"
"X1"
(-B-√D)÷(2A)→X

"X2"
(-B+√D)÷(2A)→Y

Else If D=0
Then "1 SOLUTION"
"X0"
-B÷(2A)→X

Else "PAS DE SOLUTION"
IfEnd
IfEnd

Prompt A,B,C
B²-4AC→D
Disp "DELTA",D
If D>0
Then
(-B-√(D))/(2A)→X
(-B+√(D))/(2A)→Y
Disp "2 SOLUTIONS "
Disp X,Y
Else
If D=0
Then
Disp "1 SOLUTION"
-B/(2A)→X
Disp X
Else
Disp "PAS DE SOLUTION"
End
End

Signe d'un trinôme du second degré

Propriété :
Soit

f

une fonction polynôme de degré 2 de la forme :

f (x) = a x ² + b x + c

avec $a$ ≠ 0.

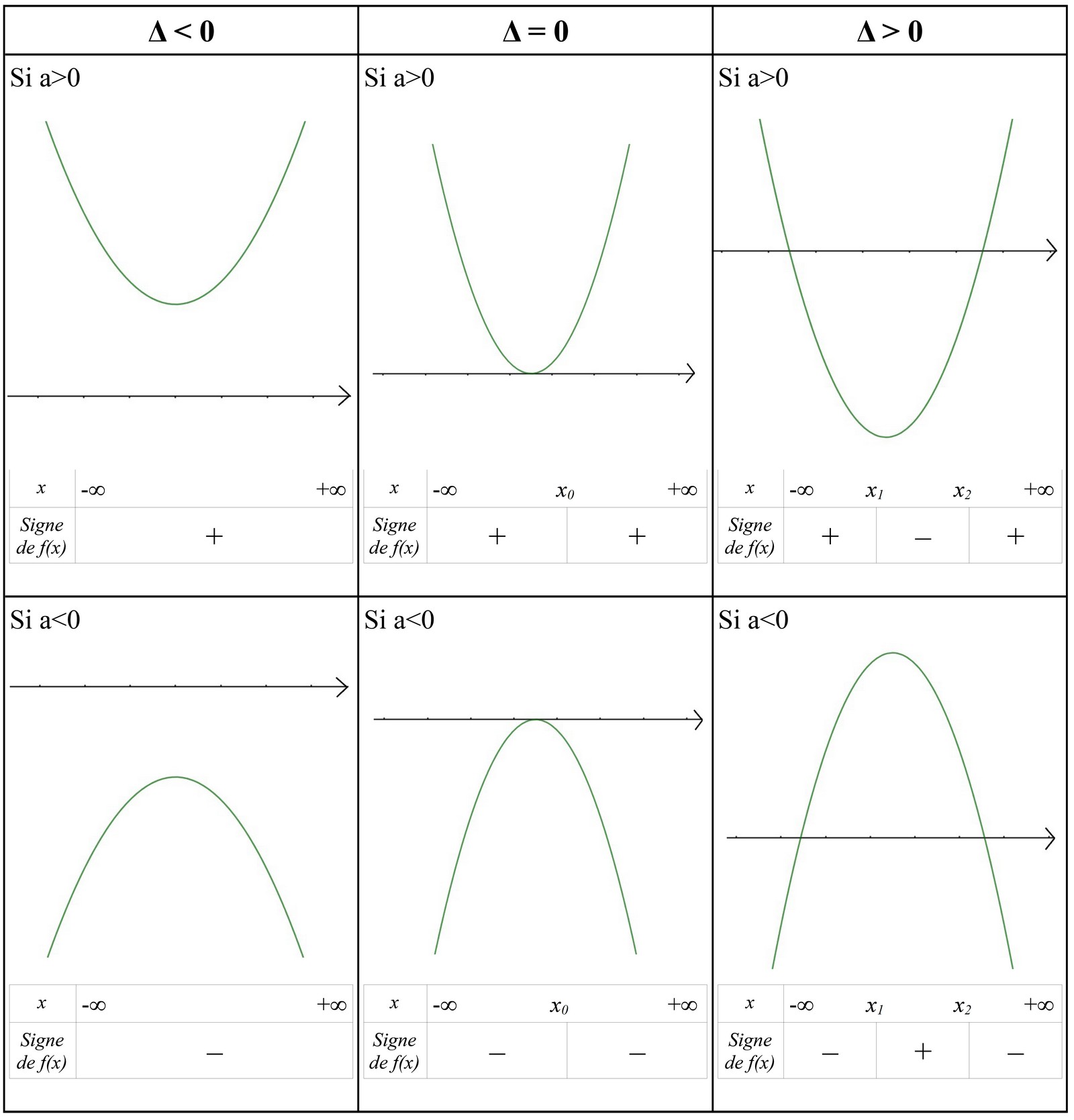
f

est toujours du signe de

a

sauf entre les racines du trinôme si elles existent.

Si Δ<0:

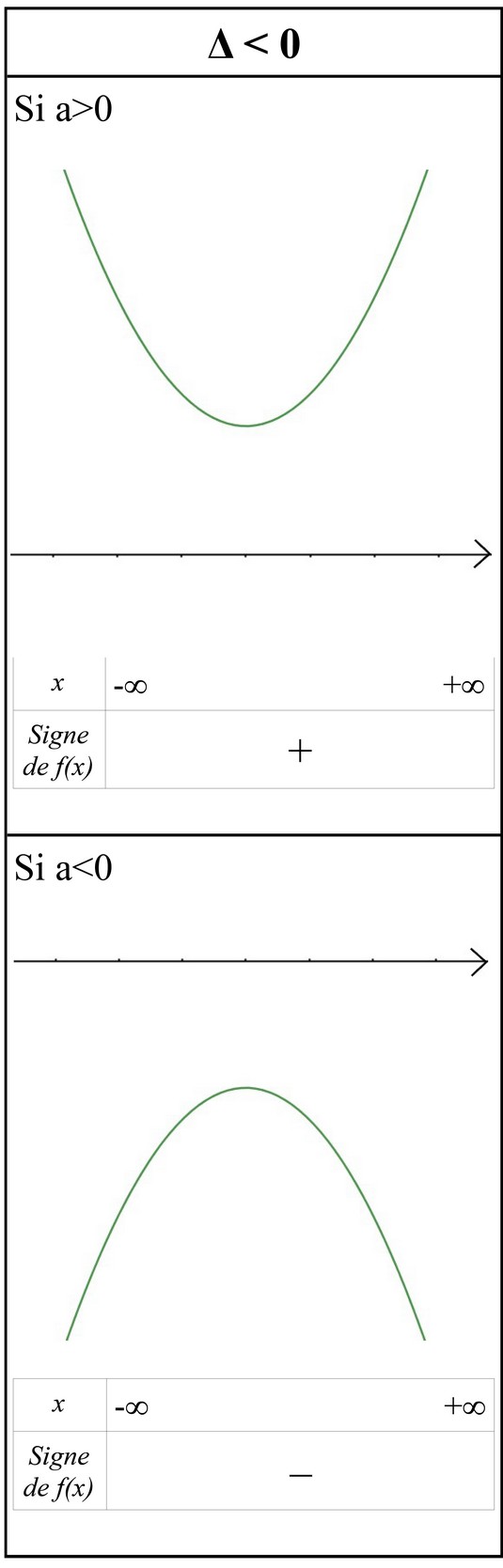
signe d un trinome du second degré de discriminant positif

Si Δ=0:

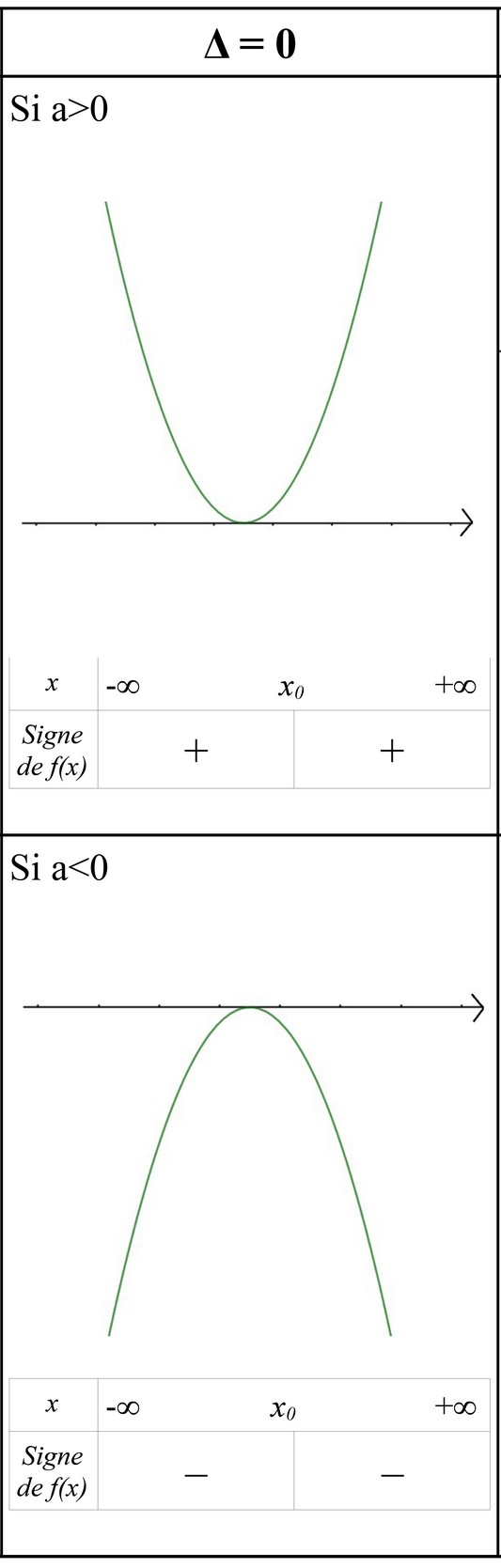
signe d un trinome du second degré de discriminant nul

Si Δ>0:

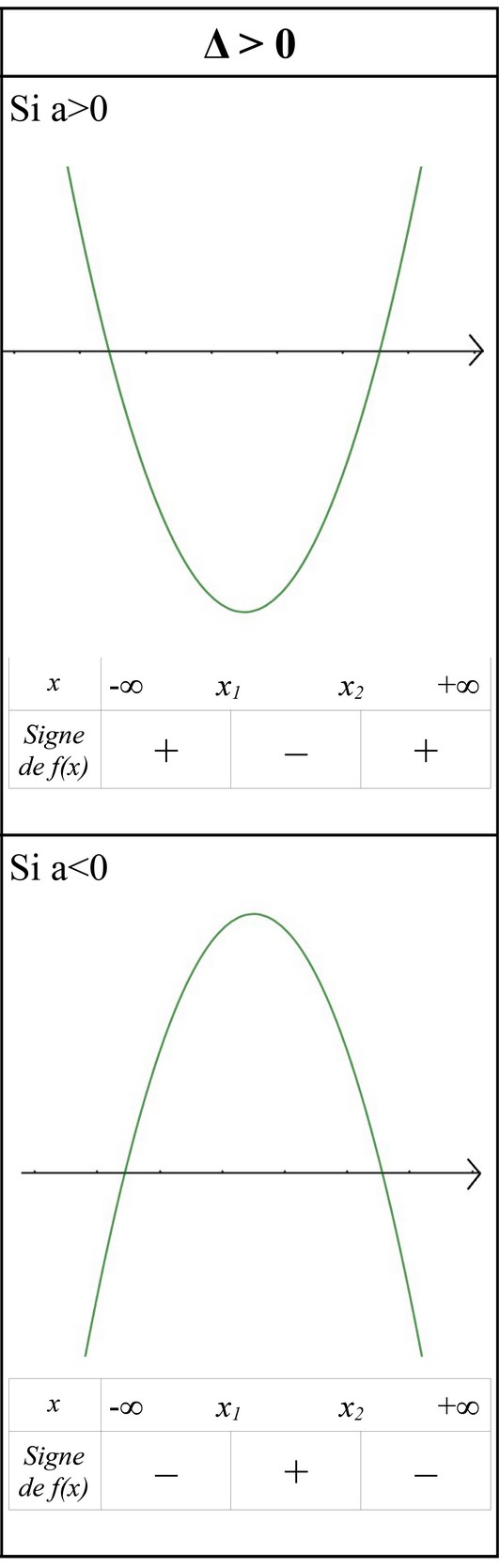
signe d un trinome du second degré dediscriminant négatif

Exemples :

a) Résoudre l'inéquation x² - 8x - 9 > 0

Solution :

a = 1 , b = -8 et c = -9.
Δ = b² - 4ac
Δ = (-8)² - 4×1×(-9)
Δ = 64-(-36) = 64 + 36 = 100
Δ > 0, donc l'équation x² - 8x - 9 = 0 admet 2 solutions:

x_{1} = \frac{8 - \sqrt{100}}{2 \times 1}

x_{1} = \frac{8 - 10}{2} = \frac{-2}{2} = -1

x_{2} = \frac{8 + \sqrt{100}}{2 \times 1}

x_{2} = \frac{8 + 10}{2} = \frac{18}{2} = 9

L'équation x² - 8x - 9 = 0 admet deux solutions : -1 et 9.
Puisque

a

est positif,

f

est positive partout sauf entre -1 et 9.

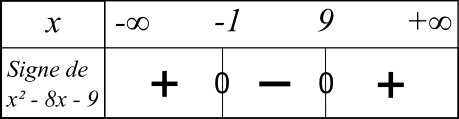
tableau de signes second degré

Donc

S = ]-∞;-1[ U ]9;+∞[

b) Résoudre l'inéquation -3x² + 2x - 1 < 0

Solution :

a = -3 , b = 2 et c = -1.
Δ = b² - 4ac
Δ = (2)² - 4×(-3)×(-1)
Δ = 4-12 = -8
Δ < 0, donc l'équation -3x² + 2x - 1 = 0 n'admet aucune solution et -3x² + 2x - 1 est toujours du signe de a, quelque soit la valeur de x, donc -3x² + 2x - 1 est toujours inférieur à 0.

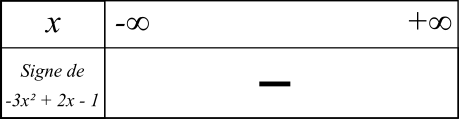
tableau de signes fonction de degré 2

Donc

S = ]-∞;+∞[ = ℝ