Cours : Equations de droites

Equations de droites

Propriété :
Dans un repère du plan, toute droite d admet une équation de la forme :

• y = mx + p, si d n'est pas parallèle à l'axe des ordonnées.
• x = k, si d est parallèle à l'axe des ordonnées.

Exemples :

d₁ est non parallèle à l'axe des ordonnées.
d₁ a pour équation y = 2 x - 1

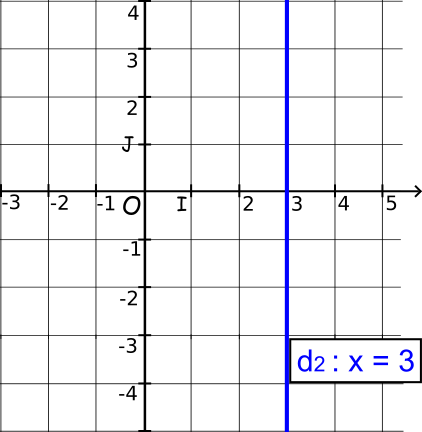
d₂ est parallèle à l'axe des ordonnées.
d₂ a pour équation x = 3

Définitions :
Soit d une droite qui admet pour équation y = mx + p.
• m est le coefficient directeur de d.
• p est l'ordonnée à l'origine de d.

Exemples :
• d : y = 2 x - 1 , le coefficient directeur de d est 2 et son ordonnée à l'origine est -1.
• d : y = 4 , le coefficient directeur de d est 0 et son ordonnée à l'origine est 4.
• d : y = -3 x , le coefficient directeur de d est -3 et son ordonnée à l'origine est 0.

Interprétation graphique :
• Le coefficient directeur indique la pente de la droite , il est positif lorsque la droite "monte", négatif lorsque la droite "descend" et égal à 0 lorsque la droite est parallèle à l'axe des abscisses.

• L'ordonnée à l'origine est égale à l'ordonnée du point d'intersection de la droite avec l'axe des ordonnées.

d₁ a pour équation y = 2 x - 1
La droite monte, le coefficient directeur est positif.
À partir de n'importe quel point de la droite, en avançant d'une unité en abscisse, on doit monter de deux unités en ordonnée pour rejoindre la droite, donc le coefficient directeur est égal à 2.

d₂ a pour équation y = 4
La droite est parallèle à l'axe des abscisse donc le coefficient directeur est nul (égal à 0).

d₃ a pour équation y = -3 x
La droite descend, le coefficient directeur est négatif.
À partir de n'importe quel point de la droite, en avançant d'une unité en abscisse, on doit descendre de trois unités en ordonnée pour rejoindre la droite, donc le coefficient directeur est égal à -3.

Calcul du coefficient directeur :
Soient A(x_A;y_A) et B(x_B;y_B) deux points distincts d'une droite d non parallèle à l'axe des abscisses. Le coefficient directeur m de la droite (AB) est égal à

\frac{y_{B} - y_{A}}{x_{B} - x_{A}}

.
Exemple : Soient A(2;-5) et B(5;1) deux points d'une droite (AB). A et B n'ont pas la même abscisse donc (AB) admet bien une équation de la forme y = mx + p et m =

\frac{1 - (-5)}{5 - 2}

\frac{6}{3}

= 2. Le coefficient directeur de la droite (AB) est égal à 2.

Tracer une droite d'équation donnée

1) Cas 1 : droite d'équation x = c.

Dans ce cas, il suffit de tracer une droite parallèle à l'axe des ordonnées passant par le point de coordonnées (0;c). En effet, tous les points de cette droite ont une abscisse égale à c.

Dans l'exemple ci-contre, la droite d₂ a pour équation x = 3, elle est donc parallèle à l'axe des ordonnées et passe par le point de coordonnées (0;3).

2) Cas 2 : droite d'équation y = mx + p.

a) En utilisant le coefficient directeur et l'ordonnée à l'origine.

Exemple : Soit d la droite d'équation y = 3x - 4.

L'ordonnée à l'origine est égale à -4, donc le point A de coordonnées (0;-4) appartient à la droite. On peut placer ce point sur le repère.

Le coefficient directeur est égal à 3, donc à partir du point A, en avançant de 1 en abscisse et en montant de 3 en ordonnée, on arrive au point B de coordonnées (1;-1).

On peut tracer la droite (AB).

b) En utilisant un tableau de valeurs.

Exemple : Soit d la droite d'équation y = - $\frac{1}{2}$ x + 2.

On peut choisir deux valeurs distinctes pour x et calculer les valeurs de y correspondantes.

Par exemple, si x=0, alors y = -

\frac{1}{2}

×0 + 2 = 2. On peut placer le point A de coordonnées (0;2).

Si x = 4, alors y = -

\frac{1}{2}

× 4 + 2 = -2 + 2 = 0. On peut placer le point B de coordonnées (4;0).

valeurs de x	0	4
y = - $\frac{1}{2}$ x + 2	2	0

On peut tracer la droite (AB).

Déterminer l'équation d'une droite passant par deux points.

Soient A(x_A;y_A) et B(x_B;y_B) deux points distincts d'une droite d.

• Si x_A = x_B, alors d est parallèle à l'axe des ordonnées et d a pour équation x = x_A.

• Si x_A = x_B, alors d a pour équation y = mx + p. On calcule d'abord le coefficient directeur (m =

\frac{y_{B} - y_{A}}{x_{B} - x_{A}}

) puis on utilise les coordonnées de A ou de B dans l'équation pour retrouver l'ordonnée à l'origine.

Exemple : Soient deux points A(-4;7) et B(1;-8). Déterminer l'équation de la droite (AB).

1) De quelle forme est l'équation ?
A et B n'ont pas la même abscisse donc la droite (AB) a pour équation y = mx + p.

2) Calcul du coefficient directeur.
m =

\frac{y_{B} - y_{A}}{x_{B} - x_{A}}

\frac{-8 - 7}{1 - (-4)}

\frac{-15}{5}

= -3.
Donc le coefficient directeur de la droite (AB) est égale à -3.

3) Calcul de l'ordonnée à l'origine.
(AB) a pour équation y = -3x + p, or A appartient à la droite, donc y_A = -3x_A + p.
Donc 7 = -3 × ( -4 ) + p, d'où 7 = 12 + p, soit p = -5.
Donc l'ordonnée à l'origine de la droite (AB) est égale à -5.

4) Conclusion.
Finalement (AB) a pour équation y = -3x - 5.