Cours : Les échelles

Lorsqu'on effectue un agrandissement ou une réduction, les longueurs obtenues sont proportionnelles aux longueurs de départ. On appelle échelle le coefficient de proportionnalite permettant de passer des distances réelles aux distances sur le plan, exprimées dans la même unité:

échelle = \frac{longueur sur la carte ou le plan}{longueur réelle}

Cas de la réduction

Pour faire une carte ou un plan, on effectue la plupart du temps une réduction de la réalité. Les dimensions sur la carte ou le plan sont proportionnelles aux dimensions réelles.

Exemples :
1) Calculer une échelle

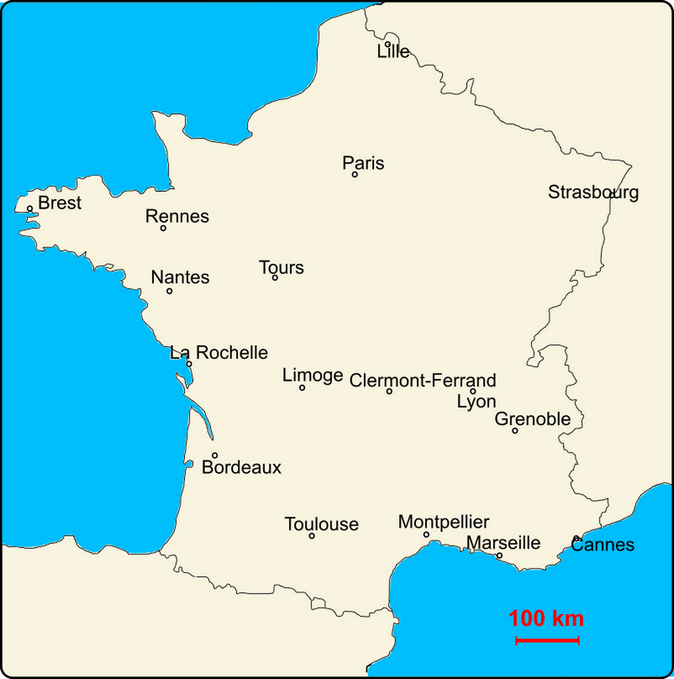
Sur la carte ci-contre, le segment rouge en bas à droite représente 100km dans la réalité. Supposons qu'il mesure 1cm (Attention, ce n'est peut-être pas le cas sur votre écran).
100km = 10 000 000cm, donc l'échelle de cette carte est :

échelle = \frac{1}{10 000 000}

cela signifie que les dimensions sur la carte sont 10 millions de fois plus petites qu'en réalité.

2) Utiliser une échelle : calculer une distance réelle

Énoncé : Une carte est représentée à l'échelle

\frac{1}{100 000}

. Deux villes sont distantes de 7cm sur cette carte. Quelle est la distance réelle entre ces deux villes ?

Réponse :Soit x la distance réelle entre les deux villes en cm. Le tableau suivant est un tableau de proportionnalité :

Distance sur la carte (en cm)	1	7
Distance réelle (en cm)	100 000	x

x = 7 \times 100 000 = 700 000

700 000 cm = 7km. Les deux villes sont distantes de 7km.

3) Utiliser une échelle : calculer une distance sur un plan.
Énoncé :Un plan est représenté à l'échelle

\frac{1}{250}

. Un mur mesure 20m dans la réalité, quelle est la longueur de ce mur sur le plan ?

Réponse :20m = 2 000cm. Soit x la longueur du mur sur le plan. Le tableau suivant est un tableau de proportionnalité :

Distance sur le plan (en cm)	1	x
Distance réelle (en cm)	250	2 000

x = 2000 \div 250 = 8

Le mur mesure 8cm sur le plan.

Cas de l'agrandissement

Pour représenter de très petits objets ou des petits animaux, on effectue un agrandissement de la réalité. Les dimensions obtenues sont alors proportionnelles aux dimensions réelles.

Exemples :
1) Calculer une échelle

Sur l'image ci-contre, le segment rouge en bas à droite représente 2mm dans la réalité. Supposons qu'il mesure 1cm (Attention, ce n'est peut-être pas le cas sur votre écran).
2mm = 0,2cm donc l'échelle de cette image est :

échelle = \frac{1}{0,2} = 5

L'échelle de l'image est égale à 5, cela signifie que les dimensions sur l'image sont 5 fois plus grande qu'en réalité.

2) Utiliser une échelle : calculer une distance réelle
Énoncé : En supposant que l'échelle de cette image est égale à 5 et que la longueur de la fourmi sur l'image est égale à 3,5cm, quelle est la longueur réelle de cette fourmi?

Réponse : L'échelle de cette image est égale à 5, cela signifie que les dimensions sur l'image sont 5 fois plus grande qu'en réalité.
3,5 ÷ 5 = 0,7. Donc cette fourmi mesure 0,7 cm.

3) Utiliser une échelle : calculer une longueur sur un agrandissement.
Énoncé :En supposant que l'échelle de cette image est égale à 5 et que la distance entre les deux antennes de la fourmi est égale à 3mm dans la réalité, quelle est cette longueur sur cette image?

Réponse : L'échelle de cette image est égale à 5, cela signifie que les dimensions sur l'image sont 5 fois plus grande qu'en réalité.
3 × 5 = 15. Donc la distance entre les deux antennes sur le plan est égale à 15mm, c'est à dire 1,5cm.