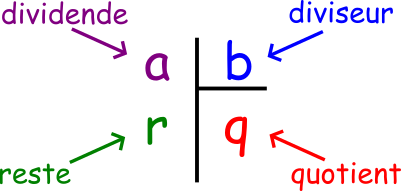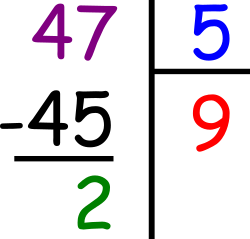Définition : Soient a et b deux nombres entiers, avec b ≠ 0.
Effectuer la division euclidienne de a par b, c'est trouver deux nombres entiers q et r tels que a = b × q + r avec r < b.
Vocabulaire :


Exemple :

Multiples et diviseurs :
Lorsque le reste d'une division euclidienne est nul, on dit que le dividende est un multiple du diviseur. Si a = b × q, alors a est un multiple de b.

Vocabulaire :
On dit aussi :
• b est un diviseur de a .
• a est divisible par b.
• b divise a.

Exemple :


Remarques :
• Tout nombre entier a au moins deux diviseurs : 1 et lui-même.
• Tout nombre entier non nul est un diviseur de 0.

Critères de divisibilité :
Un critère de divisibilité est une méthode qui permet de savoir facilement si un nombre entier est divisible par un autre nombre entier.
Règles :
• Un nombre est divisible par 2 si son chiffre des unités est 0; 2; 4; 6 ou 8
• Un nombre est divisible par 5 si son chiffre des unités est 0 ou 5
• Un nombre est divisible par 10 si son chiffre des unités est 0
• Un nombre est divisible par 3 si la somme de ses chiffres est divisible par 3
• Un nombre est divisible par 9 si la somme de ses chiffres est divisible par 9
• Un nombre est divisible par 4 si le nombre formé par ses deux derniers chiffres est divisible par 4
Exemple :
• 1848 se termine par 2 donc 1848 est un multiple de 2 mais pas de 5, ni de 10.

• La somme des chiffres de 1848 est égale à 21 (1 + 8 + 4 + 8 =21). Or 21 est un multiple de 3 mais pas de 9 donc 1848 est un multiple de 3 mais pas de 9.

• 1848 se termine par 48 et 48 est divisible par 4 donc 1848 est divisible par 4.