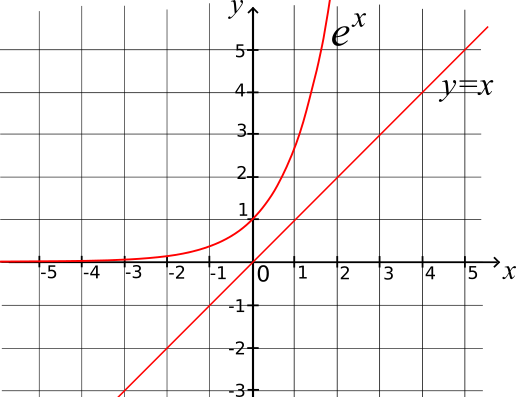
Lorsque x tend vers +∞, e^x tend vers +∞, donc $\underset{x\text{→+∞}}{lim<!--limite-->}\frac{e^x}{x}$ est une forme indéterminée. Cependant, en observant les courbes représentatives de x↦x et x↦e^x, on constate que la courbe de la fonction exponentielle croit beaucoup plus rapidement. Intuitivement, on dirait que la fonction exponentielle l'emporte sur x à l'infini. C'est effectivement le cas et $\underset{x\text{→+∞}}{lim<!--limite-->}\frac{e^x}{x}=\text{+∞}$ (voir démonstration plus bas)


Propriétés :


Démonstration de la propriété 1 :
1) Résultat préliminaire : Montrons que pour tout x ∈ ℝ, on a e^x>x.
Soit f, la fonction définie sur ℝ par f(x)= e^x-x.
f est dérivable sur ℝ et f'(x)= e^x-1
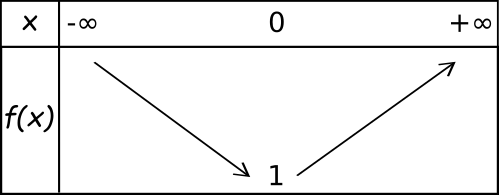
f' s'annule en 0, f'(x)<0 sur ]-∞;0[ et f'(x)>0 sur ]0;+∞[, on obtient donc le tableau de variations ci-dessous:

D'après le tableau de variations de f, pour tout x∈ℝ, f(x)≥1 , donc f(x)>0 et donc e^x>x.

2) Montrons que pour tout x >0, $\frac{e^x}{x}>\frac{x}{4}$.
Soit x un réel strictement positif. D'après le résultat préliminaire, $e^{\frac{x}{2}}>\frac{x}{2}$ et donc, en divisant par $\sqrt{x}$, $\frac{e^{\frac{x}{2}}}{\sqrt{x}}>\frac{\sqrt{x}}{2}$. En élevant chaque membre au carré, on obtient $\frac{e^x}{x}>\frac{x}{4}$ (car si a >b>0, alors a²>b²).
Or $\underset{x\text{→+∞}}{lim<!--limite-->}\frac{x}{4}=\text{+∞}$, donc $\underset{x\text{→+∞}}{lim<!--limite-->}\frac{e^x}{x}=\text{+∞}$

Propriétés :
Pour tout entier naturel n, on a

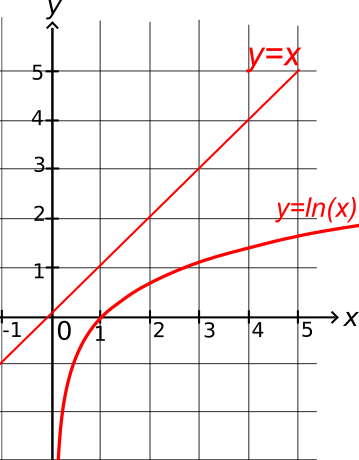
De même, lorsque x tend vers +∞, ln(x) tend vers +∞, donc $\underset{x\text{→+∞}}{lim<!--limite-->}\frac{\text{ln(}x\text{)}}{x}$ est une forme indéterminée. Cependant, en observant les courbes représentatives de x↦x et x↦ln(x), on constate que la courbe de la fonction logarithme croit beaucoup moins rapidement. Intuitivement, on dirait que x l'emporte sur la fonction logarithme à l'infini. C'est effectivement le cas et $\underset{x\text{→+∞}}{lim<!--limite-->}\frac{\text{ln(}x\text{)}}{x}=0$


Propriétés :

Propriétés :
Pour tout entier naturel n≥2, on a

Exercice :
Limites - Croissance comparée
Limites de fonctions avec logarithme