Approche graphique de la convexité
Définition :
Soit
f une fonction définie sur un intervalle
I et
C sa courbe représentative dans un repère.
•
f est
convexe sur
I si pour tous réels a et b appartenant à
I,
C est en-dessous de la sécante (AB) ( avec A(a;f(a)) et B(b;f(b)) ) sur l'intervalle [a;b].
•
f est
concave sur
I si pour tous réels a et b appartenant à
I,
C est au-dessus de la sécante (AB) ( avec A(a;f(a)) et B(b;f(b)) ) sur l'intervalle [a;b].
Exemples :
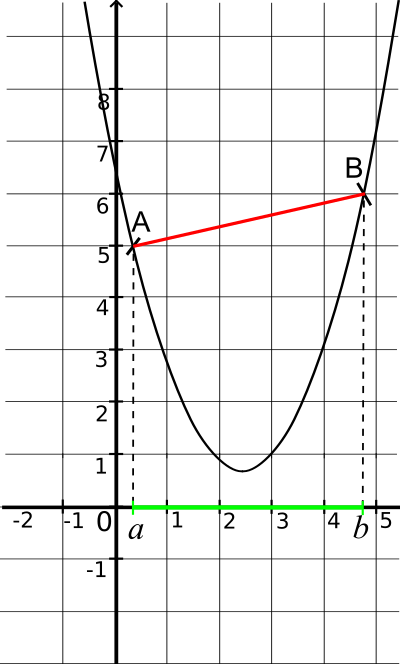 Représentation graphique d'une fonction convexe
Représentation graphique d'une fonction convexe
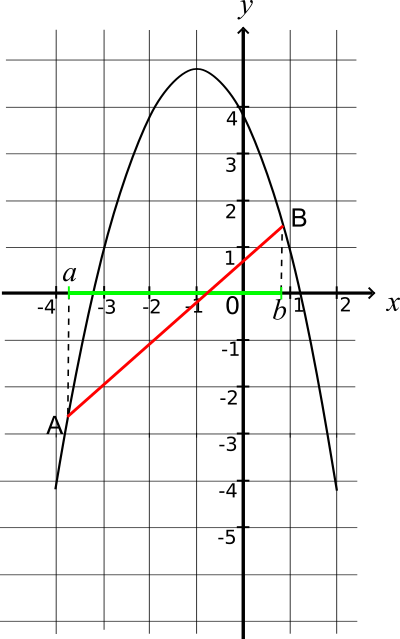 Représentation graphique d'une fonction concave
Représentation graphique d'une fonction concave
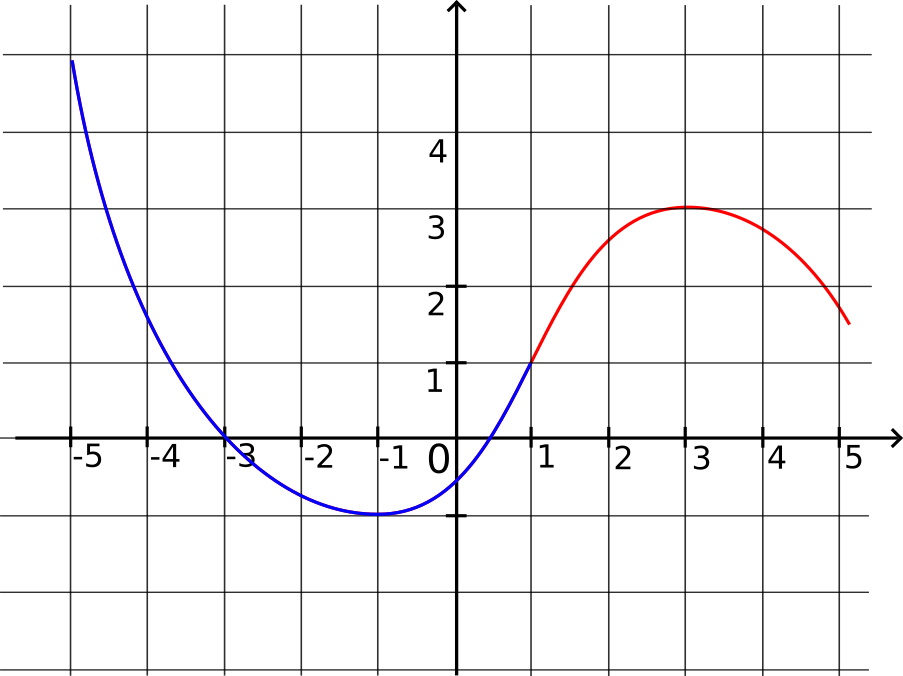 Représentation graphique d'une fonction convexe (en bleu) puis concave (en rouge)
Représentation graphique d'une fonction convexe (en bleu) puis concave (en rouge)
Définition :
Soit
f une fonction définie et dérivable sur un intervalle
I ,
C sa courbe représentative et A(a; f(a)) un point de
C.
A est un
point d’inflexion de
C si la tangente à
C en A traverse
C en A.
Propriété :
Soit
f une fonction définie et dérivable sur un intervalle
I et
C sa courbe représentative et A(a; f(a)) un point de
C.
A est un
point d’inflexion de
C si la fonction
f change de convexité en A.
Exemples :
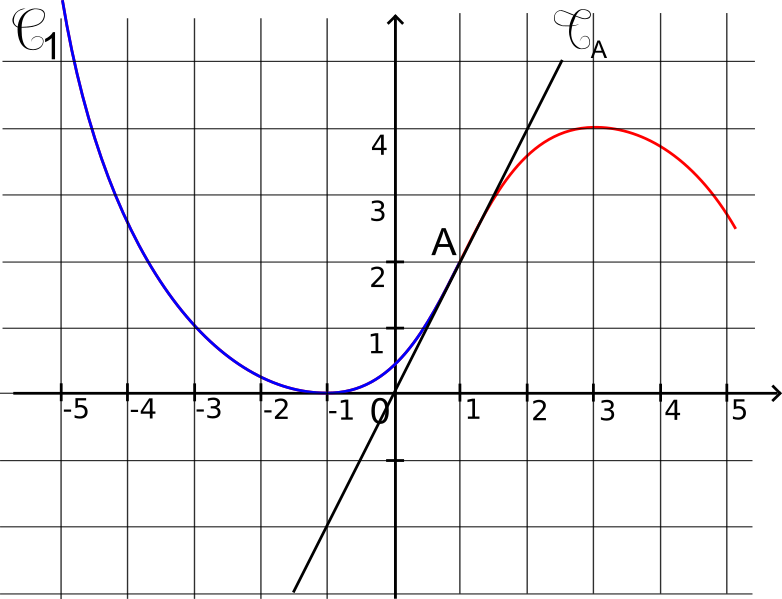 Cf est la courbe représentative d'une fonction f.
Cf est la courbe représentative d'une fonction f.
Le point A(1;2) est un point d'inflexion de la courbe Cf
f est convexe sur [-5;1] puis concave sur [1;5]
La tangente à Cf au point A traverse la courbe Cf
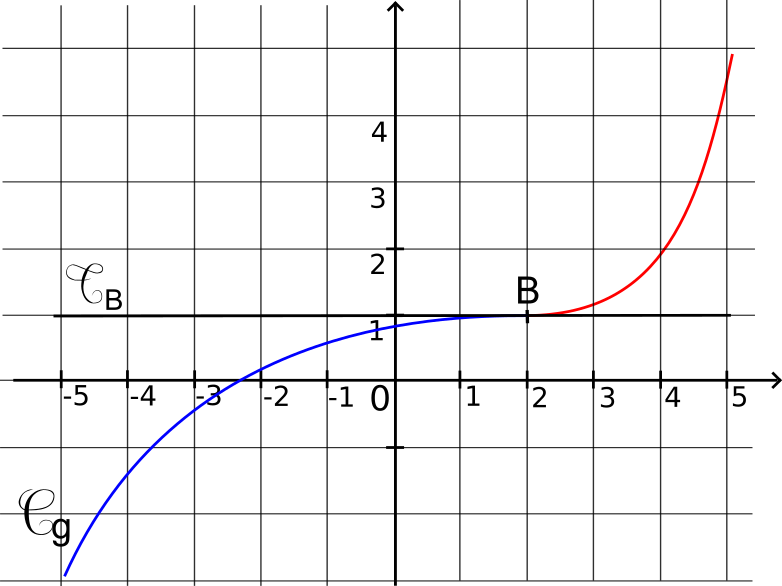 Cg est la courbe représentative d'une fonction g.
Cg est la courbe représentative d'une fonction g.
Le point B(2;1) est un point d'inflexion de la courbe Cg
g est concave sur [-5;2] puis convexe sur [2;5]
La tangente à Cg au point B traverse la courbe Cg
Convexité des fonctions dérivables
Propriété :
Soit
f une fonction deux fois dérivable sur un intervalle
I.
•
f est
convexe sur I si et seulement si
f'' est
positive sur I
•
f est
convexe sur I si et seulement si
f' est
croissante sur I
De même :
•
f est
concave sur I si et seulement si
f'' est
négative sur I
•
f est
convexe sur I si et seulement si
f' est
décroissante sur I
Exemple :
Soit
f la fonction définie sur ℝ par
f(x) = -7
x² + 3
x - 2
f est deux fois dérivable sur ℝ et
f''(x)= -14
f'' < 0 sur ℝ donc f est concave sur ℝ
Propriété :
Soit
f une fonction deux fois dérivable sur un intervalle
I et
C sa courbe représentative dans un repère.
•
f est convexe sur
I si et seulement si
C est au-dessus de toutes ses tangentes.
•
f est concave sur
I si et seulement si
C est en dessous de toutes ses tangentes.
Exemples :
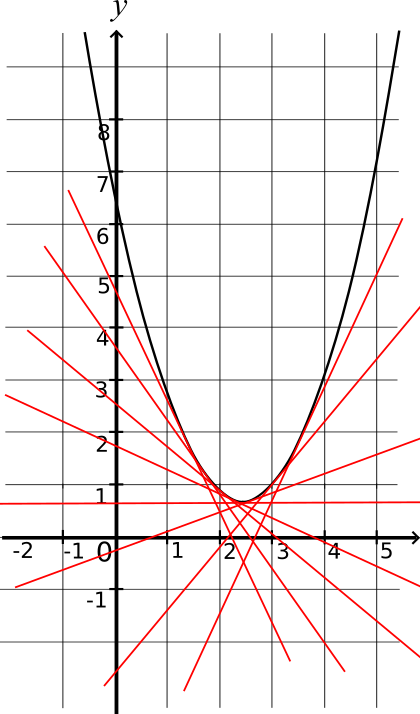 Représentation graphique d'une fonction convexe
Représentation graphique d'une fonction convexe
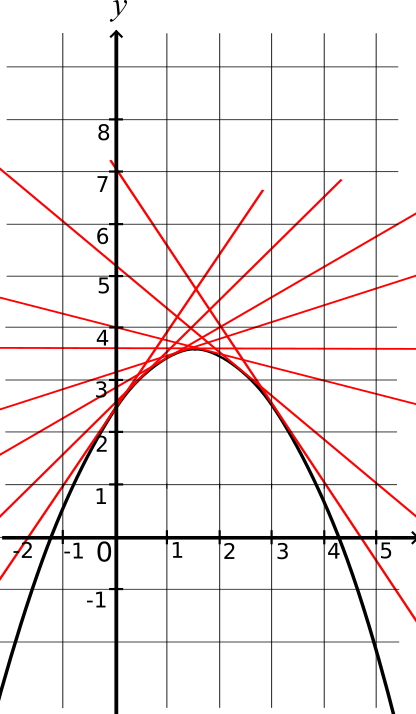 Représentation graphique d'une fonction concave
Représentation graphique d'une fonction concave
Propriété :
Soit
f une fonction deux fois dérivable sur un intervalle
I,
C sa courbe représentative dans un repère et a un réel appartenant à
I.
• Si
f' change de variations en a, alors
C admet un point d'inflexion au point d'abscisse a.
• Si
f'' s'annule en changeant de signe en a, alors
C admet un point d'inflexion au point d'abscisse a.
Exemple :
Soit
f, la fonction définie sur ℝ par
pour tout
et
pour tout
donc la courbe représentative de
f admet un point d'inflexion au point d'abscisse -5.
Remarque : la courbe représentative d'une fonction peut admettre un point d'inflexion en a lorsque
f''(a) n'existe pas.
Exemple :
Soit
f, la fonction définie sur ℝ par
n'existe pas.
pour tout
et
pour tout
donc la courbe représentative de
f admet un point d'inflexion au point d'abscisse 0.










